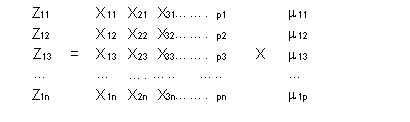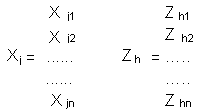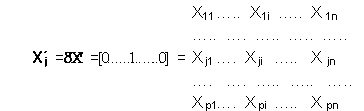|
Una de las principales actividades realizadas en el desarrollo de la investigación fue la selección y construcción de indicadores que expliquen los niveles de vida alcanzados por una población en un ámbito determinado. Como es lógico, tuvimos en primer lugar las restricciones que impone la información disponible. La información sobre los niveles de vida ha sido tomada de la encuesta ENAHO realizada durante el cuarto trimestre de 1998. La información de base para el análisis del año 1993, fue tomada de una muestra del 5% del Censo de Población y Vivienda. Dicha muestra fue seleccionada por el INEI y los resultados alcanzados se acercan con un pequeño margen de error al obtenido a través del Censo. Desde el punto de vista metodológico, las actividades desarrolladas en la investigación fueron las siguientes: 1) Selección de la Unidad de Análisis. 1) Selección de la Unidad de Análisis. La unidad de análisis considerada en ambas encuestas fue el Hogar. Sin embargo para fines del estudio, se consideró necesario analizar el nivel de vida alcanzado por los hogares en un ámbito geográfico determinado. Para el análisis multivariante es muy importante trabajar con agregados de poblaciones, ya que ellos permiten que los datos empíricos y los resultados obtenidos, puedan ser contrastados con la realidad. Los datos censales del CPV, por tratarse de datos censales no ofrecen restricciones para trabajar con agregados de poblaciones. Los indicadores pueden ser calculados a nivel de distrito, provincia, región natural, departamentos etc. La restricción en este sentido, se debe a Encuesta ENAHO-98 ya que con base a las características de diseño, se puede inferir a 8 dominios: Costa Norte, Costa Centro (excepto Lima Metropolitana), Costa Sur, Sierra Norte, Sierra Centro, Sierra Sur, Selva y Lima Metropolitana. 2) Selección de Indicadores Una de las primeras actividades en la aplicación concreta del método propuesto, es la selección de indicadores, que demuestren, expliquen , condicionen o sean determinantes en la identificación del nivel de vida alcanzado por la población y en el caso que nos compete, indicadores relacionados a la vivienda y la salud. La selección de los indicadores depende por lo tanto, en primer lugar de un fundamento teórico que relaciona al indicador con el aspecto estudiado y demuestre su relevancia en dicho aspecto, como un indicador del nivel de vida. El sustento teórico por el cual se han seleccionado los indicadores simples para medir los niveles de vida y forma particular la vivienda, se estableció en el Capitulo IV del Informe Final. En este acápite presentaremos la definición de los indicadores seleccionados, los cuales han sido elaborados para 1993, en base a una muestra al 5% del último Censo de Población y Vivienda y para 1998 en base a la ENAHO IV trimestre. Los indicadores son : La selección de indicadores está restringida por lograr la comparabilidad de los mismos. Ello implica que no solo tienen que ser fruto de la misma metodología empleada en su procesamiento y construcción sino en la misma toma de información. En ello va incorporado no solo los conceptos utilizados, sino en las preguntas formuladas y la forma como fueron obtenidas las respuestas. La formulación de las preguntas, la construcción de los indicadores y lo supuestos utilizados afectan no solo las comparaciones intertemporales sino también los resultados de corte transversal Con estas limitaciones, que imponen de un lado la ENAHO y de otro el CPV 93, se seleccionaron indicadores que puedan ser calculados en base a ambas encuestas y se calculó su valor en cada uno de las ámbitos de inferencia de la ENAHO 98-IV. Los indicadores seleccionados fueron los siguientes: a) Indicadores de Vivienda i. Porcentaje de hogares en viviendas sin servicio de agua - HVSA. Cuantifica la proporción de hogares en viviendas particulares con ocupantes presentes que no tienen agua de red pública y de pozo. Se calcula respecto al total de hogares censados. ii. Porcentaje de hogares en viviendas sin servicio de agua ni desague - HVSAD. Cuantifica la proporción de hogares en viviendas particulares con ocupantes presentes que no tienen agua de red pública y de pozo, ni desague de ningún tipo. Se calcula respecto al total de hogares censados. iii. Porcentaje de hogares en viviendas sin alumbrado eléctrico - HVSE
Es la proporción de hogares en viviendas particulares con ocupantes presentes, que no están conectadas a la red de alumbrado pública. Se calcula respecto al total de hogares censados. iv. Porcentaje de hogares en viviendas con piso de tierra - HVCPT. Cuantifica la proporción de hogares en viviendas particulares con ocupantes presentes cuyo piso de la vivienda es de tierra. Se calcula respecto al total de hogares censados. v. Porcentaje de hogares en viviendas con hacinamiento - VCHAC. Cuantifica la proporción de hogares en viviendas particulares cuyo número de miembros por habitación es mayor o igual que tres. No se consideran como habitaciones la cocina, el baño, los pasadizos. Se calcula respecto al total de hogares censados. b) Indicadores de educación i. Tasa de analfabetismo de la población de 15 y mas años. - POANA15 Es la Proporción de la población de 15 años y más de edad que en el momento de la encuesta declaró no saber leer ni escribir. Se calcula respecto al total poblacional de ese mismo grupo de edad. ii. Promedio de años de estudio de la población de 15 años y mas -PROMAE Este indicador señala el número promedio de años de estudio aprobados por la población de 15 y más años de edad. El valor puede variar de 0 hasta 16. iii. Porcentaje de Jefes de Hogar con primaria incompleta o menos - JHOCPI Es la proporción de Jefes de Hogar que tienen a lo más el 4to grado de primaria. Se calcula respecto al total de Jefes de Hogar. iv. Porcentaje de Hog. con niños de 6 a 12 años que no asisten a la escuela - HCNAE Es el Porcentaje de hogares con presencia de al menos un niño de 6 a 12 años que no asiste a un centro educativo. v. Porcentaje de pob. fem. de 15 y mas años con Secund. completa o mas - PFCSCM. Es la proporción de mujeres de 15 y mas años de edad que declararon en las encuestas haber aprobado como mínimo la secundaria completa o mas. Se calcula respecto al total de mujeres de 15 y mas años. c) Indicadores de empleo e ingreso i. Porcentaje de la poblacion ocupada de 15 años y mas, que son trabajadores familiares no remunerados - P15TFN. Es la proporción de personas de 15 años y más que en la fecha de las encuestas declararon trabajar colaborando con otro miembro de la familia que sea patrono o independiente, sin recibir remuneración monetaria. Se expresa como un porcentaje, respecto al total de la población económicamente activa ocupada de 15 años y más. ii. Porcentaje de Hogares sin artefactos eléctricos - HVSAEL Este indicador señala la proporción de hogares en los que no tiene ninguno de los siguientes artefactos: Radio, televisor blanco y negro, televisor a color equipo de sonido, videograbadora, lavadora de ropa, refrigeradora, aspiradora y lustradora, está calculado sobre el total de hogares censados iii. Porcentaje de la población económicamente activa ocupada de 15 años y mas con primaria incompleta o menos - P15PI1. Es la proporción de la PEA ocupada de 15 años y más que en la fecha de las encuestas declaró haber aprobado a lo más el 4to grado de primaria. Se calcula respecto al total de la PEA ocupada de 15 años y más. iv. Porcentaje de la poblacion ocupada de 15 años y más en establecimientos con menos de 5 trabajadores - P15E5T. Es la proporción de la población económicamente activa ocupada de 15 años y más, que en la fecha de censo declaró trabajar en establecimientos de menos de 5 trabajadores, calculado respecto al total de la población económicamente activa ocupada de 15 años y más. v. Porcentaje de la población ocupada de 15 mas asalariada - IP15AS Este indicador señala la proporción de la población económicamente activa ocupada de 15 años y más, que participa en la actividad económica del país como trabajadores asalariados, es decir, que en la fecha de las encuestas declararon trabajar como obrero o empleado. Se calcula respecto al total de la población económicamente activa ocupada de 15 años y más. 3) Cálculo de Indicadores simples a) Cálculo de Indicadores año 1993 con base al CPV. Para el cálculo de los indicadores del Censo de Población y Vivienda se tomó como referencia, de un lado una muestra del 5% del Censo y de otro los resultados Censales publicados a nivel distrital. Como en la muestra del 5% del CPV no existía como variable los dominios de inferencia de la ENAHO (a pesar que el Censo es el marco muestral de la ENAHO), la primera acción fue incorporar dicha variable en la muestra. Ello fue realizado en base a una tabla proporcionada por la Direccion de Informatica del INEI. Según la tabla, a cada distrito sólo le era asignado un dominio. La tabla fue contrastada con la información de la ENAHO del IV trimestre 98 con resultados favorables. Sólo 2 distritos tenían asignado a la vez códigos de dominios diferentes. Asimismo los códigos de distrito usados en la tabla se encontraban en la Encuesta ENAHO 98-IV y pertenecía a los mismos dominios. Concluida la verificación se elaboró un programa de computo elaborado en FOXPRO, a fin de asignar los códigos de dominio a la muestra del CPV, que tenia 2 tipos de archivos; el primero referido hogares (CENSOVIV.DBF) y el segundo a toda la población (CVTIP2.DBF). Con los programas de computo que se adjuntan al final del presente informe, ASIGNA1.PRG y ASIGNA2.PRG se asignaron los códigos de dominio a los archivos mencionados. Como algunos distritos que no estaban en la tabla y si en la muestra del 5% del CPV, no les fue asignado un dominio, nos remitimos una Publicación elaborada por el INEI sobre los Centros Poblados a nivel de distrito, de 1994 en base a la cual se culminó con la asignación de códigos. En base a las bases de datos CVTIP2 y CENSOVIV se calcularon las siguientes variables, a nivel de distrito: i. Total de Hogares Estas variables fueron guardadas en una base de datos denominada "Distrito", con el programa DISTRITO.PRG que se adjunta al final del presente in forme. El valor de las variables calculadas fue expandida considerando que se trataba de una muestra del 5% del CPV. Con la finalidad de obtener los indicadores a nivel de los dominio de la ENAHO, se tomó en consideración la información a nivel distrital publicada por el INEI, en el documento "Perú: Mapa de Necesidades Básicas Insatisfechas de los Hogares a nivel Distrital". Preparado por la Dirección Técnica de Demografía y estudios Sociales en Noviembre de 1994. Como en dicha publicación los indicadores seleccionados se encuentran por distrito, y son establecidos en porcentajes, se requería conocer cuantos hogares o población estaba realmente involucrada en las características establecidas por los indicadores. Por esta razón, con las variables calculadas debidamente expandidas, se creo una hoja de calculo denominada INDICA1.XLS, que se adjunta en diskette. En ella se recalculó en términos de población y de hogares, los indicadores a fin de poderlos agregar a nivel de cada dominio. Posteriormente en base a tablas dinámicas se calculó en términos de hogares y población los indicadores a nivel de dominio, para finalmente calcular los porcentajes respectivos. Los programas de cómputo denominados ASIGNA1 Y ASIGNA2, así como la hoja de cálculo INDICA1.xls se adjuntan tambien en diskette al presente informe. El valor de los indicadores simples calculados se presentan en los Cuadro 6.1, 6.2 y 6.3 del Informe final. b) Cálculo de Indicadores del año 1998 con base a la ENAHO -IV. Los indicadores fueron calculados en base al Programa SPSS vs 7.5 para Windows. Como los hogares tenia diferentes probabilidades de ser elegidos, la muestra fue expandida en base a los factores de expansión, tomando en cuenta para el calculo de los indicadores pertinentes, sólo la población en hogares. El Programa VIV-984.sps se adjunta al final del presente informe y se ha grabadoi asimismo en diskette. Al igual que los indicadores para al año 93, el valor de los indicadores simples calculados en base a ENAHO para 1998, se presentan en los Cuadro 6.1, 6.2 y 6.3 del Informe final. 4) El Método de Componentes principales. A partir de los indicadores simples y su análisis descriptivo, se empleó el análisis multivariado, para calcular los indicadores parciales y el indicador sintético global. Posteriormente se analizaron los resultados. a) Descripción Teórica del Método La utilidad principal del análisis de componentes principales reside, en que permite estudiar un fenómeno multidimensional, cuando algunas o muchas de las variables comprendidas en el estudio están correlacionadas entre si, en mayor o menor grado. En realidad, al estudiar un fenómeno multivariable, las correlaciones entre las variables que explican el fenómeno, se constituyen en un "velo" que impide evaluar adecuadamente el papel que juega cada variable en el fenómeno. El Análisis de Componentes Principales tiene como objetivo el hallar combinaciones lineales de variables representativas de cierto fenómeno multidimensional, con la propiedad de que exhiban varianza máxima y que a la vez estén incorrelacionadas entre si. La varianza de la componente es una expresión de la cantidad de información que lleva incorporada. Es decir cuanto mayor sea su varianza, mayor será la cantidad de información incorporada en dicha componente. Por ésta razón las sucesivas combinaciones o variantes o componentes se ordenan en forma descendente de acuerdo a la proporción de la varianza total presente en el problema, que cada una de ellas explica. La primer componente es por lo tanto, la combinación de máxima varianza; la segunda es otra combinación de variables originarias que obedece a la restricción de ser ortogonal a la primera y de máxima varianza, la tercer componente es aún otra combinación de máxima varianza, con la propiedad de ser ortogonal a las dos primeras; ..... y así sucesivamente Por sus propiedades de ortogonalidad, las sucesivas componentes después de la primera se pueden interpretar como las combinaciones lineales de las variables originarias que mayor varianza residual explican, después que el efecto de las precedentes ha sido ya removido y así sucesivamente hasta que el total de varianza ha sido explicado. Es posible que unas pocas primeras componentes logren explicar una alta proporción de la varianza total; en este caso que ocurre cuando las variables están correlacionadas en mayor grado, las componentes pueden sintéticamente sustituir a las múltiples variables originarias. Ello permitiría resumir en unas pocas variantes o componentes no correlacionadas gran parte de la información originaria. Desde este punto de vista, el método de componentes principales es considerado como un método de reducción, ya que puede reducir la dimensión del numero de variables que inicialmente se han considerado en el análisis. b) Obtención de las componentes principales En primer lugar, es necesario indicar que la obtención de componentes principales es un caso típico de cálculo de raíces y vectores característicos de una matriz simétrica. Esta matriz simétrica es la conformada por la matriz de correlaciones de las variables consideradas en el estudio del fenómeno multidimensional. i) Obtención de la primera componente Consideremos que disponemos de una muestra de n observaciones sobre el comportamiento de p variables X La primera componente al igual que las siguientes, se expresa como combinación lineal de las variables originales, es decir: Z1i = m 1 1 C 1 i + m 1 2 C 2 i +…………… +m 1 p C p1
Donde Z 1i es el valor de la componente Z1 para la observación i. Asimismo, X1i X2i X3i son los valores de las variables X1, X2 , X3 , en la observación i. Finalmente m11, m12, m13, … m1p es el vector de pesos o coeficientes cuyo valor queremos determinar.Para el conjunto de las n observaciones muestrales esta ecuación se puede expresar matricialmente de la siguiente forma:
Si la expresamos en forma vectorial tenemos: Z1 = X m 1La primera componente es obtenida de forma que su varianza sea máxima, sujeta a la restricción de que la suma de los pesos ( m1j) al cuadrado, sea igual a la unidad.La varianza de la primera componente, dada por: Var (Z1) = ( S Z21i ) / n = ( z´1 z1 ) / n = ( m ´1 X´ X m 1 ) / n = m ´1 ( X´ X) / n m 1ya que la media de las Z Si las variables están expresadas en desviaciones respecto a la media ( 1/n) X´X es la matriz de covarianza de las Xj variables. Si las variables están tipificadas (1/n) X´X es igual a la matriz de correlaciones. Si denominamos a la matriz X´X como V, la varianza de la primera componente seria : Var (Z1) = m ´1 V m 1
Si queremos que Z 1 tenga la máxima varianza tenemos que poner una restricción por que sino la varianza podría ser infinita. La restricción es que la suma de cuadrados de los coeficientes sea 1.S m 21i = m ´1 m 1 = 1Si incorporamos la restricción podemos formar el siguiente langragiano L = m ´1V m 1 - l ( m ´1 m 1 - 1 )Para maximizar el valor del lagrangiano derivamos respecto a u1 e igualamos a 0: ¶ L / ¶ u1 = 2Vm 1 - 2l m 1 = 0es decir : (V - l I ) m 1 = 0Al resolver la ecuación ½ V - l I ½ = 0 , se obtienen p raíces características. Si toma la raíz característica mayor (l1) , se puede hallar el vector característico asociado aplicando :m ´1 m1 = 1. Luego el vector de ponderaciones o pesos que se aplica a las variables originales para obtener la primera componente principal es el vector característico asociado a la raíz característica mayor de la matriz V.ii) Obtención de las restantes componentes La segunda y las demás componentes Z h expresada en forma genérica y matricial será :Z h = X m hPara su obtención, además de la restricción de que : m´ m h = 1, se imponen restricciones adicionales para asegurar que la componente h-esima sea ortogonal a todos los vectores característicos calculados previamente.m h m 1 = m h m 2 = m h m 3= ....... m h m h-1 = 0En resumen las p componentes principales que se pueden calcular son una combinación lineal de las variables originales, en las que los coeficientes de ponderación son los correspondientes vectores característicos asociados a la matriz V. Las varianzas de los componentes vienen dadas por las raices características es decir : Var Zh = m´h V m h = l h Adoptando como medida de variabilidad de las variables originales, la suma de sus varianzas, la prop. de la componente h-esima en la variabilidad total será: l h / S l hEn el caso de variables tipificadas, como la matriz de covarianzas es la matriz de correlaciones, la prop. de la componente h-esima en la variabilidad total será: l h / pc) Correlación entre las componentes principales y las variables originales La covarianza entre la variable X j y la el componente Zh.Definamos los vectores muestrales de la componente Z h y la variable X j por :
La covarianza muestral entre X j y Z h viene dada por :Cov ( X j, Z h ) = ( X´j Z h ) / nEl vector X j se puede expresar en términos de la matriz X, utilizando un vector de orden p, al que designaremos por d, que tiene 1 en la posición j-ésima y 0 en las posiciones restantes: Así
Luego, la Cov ( X j, Z h ) en términos de X y de d seráCov ( X j, Z h ) = ( d ¢ C ¢ C m h ) / n = (d ¢ V m h ) / n = d ´l h m h = l h d ´m h = l h m h jLuego la correlación existente entre la variable X j y la componente Z h es la siguiente:r jh = Cov (X j, Zh) / (Var Xj Var Zh) ½ = l h m h j / (Var Xj l h ) ½Si las variables originales están tipificadas : r jh = m h j ( l h ) ½La matriz factorial (factor matrix) esta dado por los coeficientes r j hd) Puntuaciones sin tipificar y tipificadas Una vez calculados los coeficientes m h j se pueden obtener puntuaciones Z h i es decir, los valores de las componentes correspondientes a cada observación a partir de la siguiente relación..Z h i = m h 1 X1i + m h 2 X2 i + …. + m h p X p i h= 1,2…p i= 1,2,…..nSi una componente se divide por su desviación típica se obtiene una componente tipificada. Así, designando por Y h a la componente h-ésima tipificada, esta viene definida por : Y h = Z h / ( l h ) ½ = m h 1 X1i / ( l h ) ½ + m h 2 X2 i / ( l h ) ½ +…. + m h p X p i / ( l h ) ½Como ya se ha indicado a la matriz formada por los coeficientes m h 1 / ( l h ) ½ se le denomina matriz de puntuaciones de los factores, (factor score coefficient matriz) En resumen se pueden obtener las siguientes conclusiones: 1) Las componentes principales son combinaciones lineales de las variables originales. 2) Los coeficientes de las combinaciones lineales son los elementos de los vectores característicos asociados a la matriz de covarianza de las variables originales . 3) La primera componente principal está asociada a la mayor raíz característica de la matriz de covarianzas de las variables originales. 4) La varianza de cada componente es igual a la raíz característica a que va asociada. 5) En el caso de que las variables estén tipificadas, la proporción de la variabilidad total de las variables originales captada por una componente es igual a la raíz característica correspondiente dividida por el número de variables originales. 6) La correlación entre una componente y una variable original se determina con la raíz característica de la componente y el correspondiente elemento del vector característico asociado, en el caso de que las variables originales estén tipificadas. e) Número de componentes a retener Uno de los objetivos de los Componentes principales es reducir las dimensiones del problema pasando de p variables originales a m compnentes principales siendo m < p Pero, cuantas componentes retener ? Una primera aproximación es el criterio de la media aritmética. Teniendo en consideración que la raíz característica de una componente es precisamente su varianza, se retiene a todas aquellas l h mayores que l promedio. En el caso particular de que las variables originales se encuentren tipificadas se selecciona aquellas componentes cuya raíz característica es mayor que 1. Es decir l h >1 f) Prueba de Hipótesis de las raíces características no retenidas Bajo el supuesto de que las variables originales siguen una distribución normal multivariante, se pueden formular las siguientes hipótesis relativas a las características poblacionales no retenidas: Ho : l m+1 = l m+2 = l m+3 = l m+4 …….. = l p = 0 Esta prueba se deriva de la prueba de esfericidad de Barlet y es el estadístico Q* = ( n - (2p+1) / 6 ) ( (p-m) ln l p-m - S ln l j ) Sigue una distribución Chi cuadrado con (p-m+2) (p-m+1) / 2 grados de libertad. Si Q* > X2 con (p-m+2) (p-m+1) / 2 grados de libertad se rechaza la hipótesis nula y prueba que una o mas de las raíces no retenidas son significativamente distintas de 0. 5) Aplicación práctica : Calculo del Indicador parcial de Vivienda y salud Para fines de exposición de la aplicación de la metodología, se detallará el cálculo del indicador de Vivienda, explicándose cada una de las fases de su construcción. Todos los resultados han sido obtenidos con el paquete estadístico SPSS. En este acápite se demostrará la estadística básica, el análisis de la matriz de correlaciones y finalmente los resultados obtenidos a través del Programa SPSS. Si bien no existen modelos ni técnicas multivariantes que puedan demostrar por si mismas relaciones de causa - efecto entre las variables o indicadores básicos seleccionados, si es posible a través de la estadística básica y algunos estadísticos, mostrar evidencia empírica del grado de asociación existente entre las distintas manifestaciones del nivel de vida a través de las correlaciones estadísticas. Los indicadores considerados para explicar el nivel de vida en el rubro de Vivienda son los siguientes: % de Hogares en vivienda sin servicios de agua por red de tuberia - HVSA Estos indicadores fueron calculados tanto del CPV93 como de la ENAHO 98-IV, asignándose las siguientes denominaciones a los ámbitos geográficos: CONOR93 Costa Norte año 1993 y CONOR98 Costa Norte año 1998 Una codificación análoga fue utilizada para la Costa Centro, Costa Sur, Sierra, Selva y Lima Metropolitana, así como a nivel nacional. Los resultados de la corrida en SPSS vs 7.5 son los siguientes: Factor Analysis
En esta tabla se establece, el archivo de trabajo empleado: ULTIMO.SAV, se establece asimismo que toda la información será analizada sin filtros (Filter None), sin utilizar una variable que atribuya ponderaciones (que se usa hacer inferencia de la muestra). Se establece que el número de filas en el archivo de trabajo es de 18. Respecto a los datos perdidos se seleccionó la opción Exclude cases listwise, mediante la cual se indica que las estadísticas serán basadas en casos donde no existan valores perdidos para alguna variable. Respecto a la Sintaxis, se establece que se utilizará el Análisis factorial; ya que en el SPSS se trata a las componentes principales simplemente como un método para la extracción de los factores. Dentro de los cuadros de selección se solicita la impresión de la estadística univariada de los indicadores, la matriz de correlaciones y su determinante, la inversa de ella, el deindice KMO, el Test de Barlett, la matriz de correlaciones reproducida y el score alcanzado. i) Estadística básica y normalización de los indicadores. El Cuadro Nº 1 presenta la media, desviación estándar y coeficiente de variabilidad de los indicadores de Vivienda. En el se muestra que la variable con mayor dispersión relativa es el % de Viviendas sin agua ni desague HVSAD mientras que HOGTIE es la que tiene menor dispersión relativa. Los demás indicadores tienen una variabilidad relativa dentro de estos limites. CUADRO Nº1 ESTADISTICA DESCRIPTIVA
El Cuadro N°2 presenta los datos originales sobre los indicadores de Vivienda calculados con base a las Encuestas ENAHO 1998-IV y una muestra del CPV al 5%. Los ámbitos estudiados son los dominios de inferencia de la ENAHO 98-IV y están constituidos por: Costa Norte, Costa Centro, Costa Sur, Sierra Norte, Sierra Centro, Sierra Sur, Selva, Lima Metropolitana y Nivel Nacional (Perú) . CUADRO Nº 2 INDICADORES DE VIVIENDA
Los datos en primer lugar son normalizados con la finalidad que todos tengan como media cero y varianza unitaria. Ello es necesario, dado que generalmente trabajamos con diferentes unidades de medida y el factor "tamaño" no debe afectar los resultados. El Cuadro N°3 presenta los datos estandarizados o normalizados de los indicadores de Vivienda A partir de estos datos normalizados se calcula la matriz de varianzas y covarianzas, que en el caso de datos normalizados coincide con la matriz de correlaciones. CUADRO Nº 3 INDICADORES DE VIVIENDA NORMALIZADOS
ii) Análisis de la Matriz de correlaciones y otros estadísticos En el Cuadro Nº4 se presenta la Matriz de correlaciones, en ella se puede distinguir con claridad, la alta correlación existente entre el % de Hogares que no tienen agua, con el % de Hogares que carecen tambien de agua y desague y con el % de hogares que no tienen luz. El Indicador % de hogares en viviendas con hacinamiento es el que presenta una menor correlación con los demas indicadores. Si bien no se muestra la correlación entre la tasa de mortalidad infantil y la desnutrición, (por no haber sido seleccionados), existe mucha evidencia empírica que hogares que no tienen servicios básicos como agua o un medio adecuado para la eliminación de excretas y servicio de agua por red de tuberia o pozo, determinan la ausencia de condiciones básicas de saneamiento e incrementa los riesgos de contaminación atentando principalmente contra la niñez, provocando altas tasas de morbilidad y mortalidad, por lo que se puede considerar a HVSA y HVSAD como indicadores relacionados a la salud de las personas. CUADRO Nº4 MATRIZ DE CORRELACIONES
ANTI-IMAGE MATRICES
KMO AND BARTLETT'S TEST
Además de la matriz de correlaciones, se ha calculado el determinante de dicha matriz cuya "cercanía" a cero es un buen indicador de las altas correlaciones existentes entre las variables y muestra que uno o mas indicadores podrían ser expresados como una combinación lineal de otros. El Test de Barlett que establece la prueba de hipótesis que la matriz de correlaciones es una matriz identidad, da como resultante una c 2 alta que considerando los 10 grados de libertad rechaza Ho. El Indice de adecuación de la muestra KMO que permite comparar las magnitudes de los coeficientes de correlación con las magnitudes de los coeficientes de correlacion parcial, tiene un valor de 0.784, el cual es mediano según la escala propuesta por Kaiser. Finalmente los coeficientes de la matriz de correlación antiimagen son bajos, cercanos a cero lo cual indica que los coeficientes de correlación parcial también lo son. Comprobado mediante los test de Barlett y el índice KMO que es factible desde el punto de vista técnico aplicar el análisis factorial, se calcula las raíces y vectores característicos de la matriz de Correlaciones. Cálculo de las raíces y vectores característicos Si definimos a los datos 5 indicadores considerados en el área de Vivienda como X1, X2, X3 3 …. X55 que se encuentran debidamente normalizados La primera componente Z1i al igual que las siguientes, se expresa como una combinación lineal de las variables originales, es decir: Z1i = m 1 1 C 1 i + m 1 2 C 2 i +…………… +m 1 p C p1. Donde m11, m12, m13, … m1p es el vector característico, de pesos o coeficientes cuyo valor queremos determinar. Una vez calculado m1 es posible calcular los valores de Z1 Matricialmente se puede expresar
O también Z 1 = X m1En general, tal como se indicó anteriormente al resolver la ecuación ½ V - l I ½ = 0 , se obtienen p raíces características. Si toma la raíz característica mayor ( l1 ) , se puede hallar el vector característico asociado aplicando : m´1 m1 = 1.CUADRO Nº5 VARIANZA EXPLICADA POR COMPONENTES
El Cuadro Nº5 presenta las raíces características y su aporte en la varianza total explicada. Estas raíces constituyen a su vez las varianzas de las componentes, es decir : Var Zh = Donde V es la Matriz de correlaciones, por cuanto las variables están tipificadas. Adoptando como medida de variabilidad de las variables originales la suma de sus varianzas, la proporción de la componente h-esima en la variabilidad total será: l h / S l h o lo que es lo mismo: l h / pLuego el vector de ponderaciones o pesos que se aplica a las variables originales para obtener la primera componente principal es el vector característico asociado a la raíz característica mayor de la matriz V. El Cuadro N° 6 presenta el primer vector característico, que constituye las ponderaciones que se tienen que aplicar a los datos estandarizados para hallar la primera componente principal. CUADRO Nº6 COMPONENT SCORE COEFFICIENT MATRIX
La Correlación entre las componentes principales y las variables originales es posible calcularlas mediante : r jh = m h j ( l h ) ½ Ya que las variables originales están tipificadas. La matriz factorial (factor matrix) esta dado por los coeficientes r j h representa la correlación entre la 1ra componente principal y las variables originales. Se presenta en el siguiente cuadro : MATRIX FACTORIAL
Una vez calculados los coeficientes mh j se pueden obtener puntuaciones Z h i es decir, los valores de las componentes correspondientes a cada observación a partir de la siguiente relación..Z h i = m h 1 X1i + m h 2 X2 i + …. + m h p X p i h= 1,2…p i= 1,2,…..n Si una componente se divide por su desviación típica se obtiene una componente tipificada. Así, designando por Y h a la componente h-ésima tipificada, esta viene definida por : Y h = Z h / ( l h ) ½ = m h 1 X1i / ( l h ) ½ + m h 2 X2 i / ( l h ) ½ +…. + m h p X p i / ( l h ) ½ Como ya se ha indicado, a la matriz formada por los coeficientes definidos: m h 1 / ( l h ) ½ se le denomina matriz de puntuaciones de los factores, (factor score coefficient matriz) 6) Construcción del Indicador Sinteico Global Multivariante INDIGLO y del Indicador Sintético alternativo INDIALT. El Cuadro N°7 que se adjunta consolida la información de los 3 indicadores parciales cuya suma genera el indicador sintético global multivariante denominado INDIGLO. De acuerdo a los cálculos realizados, el Indicador sintético multivariante ISM para evaluar los cambios en los niveles relativos de vida para el periodo 1993 -1998 es: INDIGLO =4.457*INDIVS + 4.337*INDIEDU + 4.586*INDIECO En este caso, INDIVS, INDIEDU y INDIECO son las tres primeras componentes principales calculadas separadamente a partir de sus respectivos indicadores simples en los ámbitos de la vivienda, educación y empleo e ingreso. Asimismo 4.457, 4.337. y 4.586 son los respectivos autovalores correspondientes a estas primeras componentes principales. Finalmente, en el Cuadro N°7 se presenta asimismo, la forma tradicional de aplicar el Análisis de Componentes principales, para construir el indicador sintético. Los 15 indicadores fueron considerados simultáneamente. En este caso de acuerdo al gráfico de la ladera, se consideró las 2 primeras componentes principales, cuyos autovalores son 12.858 y 1.085 respectivamente. Con ellos se construyeron las respectivas proyecciones de cada observación sobre cada componente cuyos valores se presentan en el mismo cuadro, en este caso el indicador tiene la siguiente formula: INDIALT = 12.858 * INDPAR1 + 1.085 * INDIPAR2 El análisis del indicador global, al ser construido como una suma ponderada de los tres indicadores parciales anteriormente descritos no presenta variaciones significativas. Sin embargo cabe indicar que el indicador parcial que mayor influencia ejerce sobre el indicador global en la mayoría de los dominios es el indicador parcial del Ingreso y empleo -INDIECO. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||