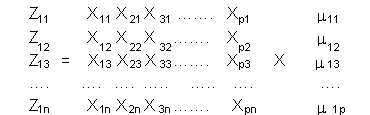Cálculo de las raíces y vectores característicos

Si definimos a los datos 5 indicadores considerados en el área de Vivienda como X1, X 2, X3 3 …. X55 que se encuentran debidamente normalizados

La primera componente Z1i al igual que las siguientes, se expresa como una combinación lineal de las variables originales, es decir:

Z1i =m 11 C 1 i + m1 2 C2 i +…………… +m 1 p C p1.

Donde m 11, m 12, m 13, … m 1p es el vector característico, de pesos o coeficientes cuyo valor queremos determinar. Una vez calculado m 1 es posible calcular los valores de Z 1

Matricialmente se puede expresar

O también

Z1 = X m1

En general, tal como se indicó anteriormente al resolver la ecuación , se obtienen p raíces características. Si toma la raíz característica mayor ( l1 ) , se puede hallar el vector característico asociado aplicando : m ´1 m1 = 1.

CUADRO Nş5.5 VARIANZA EXPLICADA POR COMPONENTES

Component

Initial Eigenvalues

Extraction Sums of Squared Loadings

Total

% of Variance

Cumulative %

Total

% of Variance

Cumulative %

1

4.457

89.133

89.133

4.457

89.133

89.133

2

.316

6.319

95.452




3

.165

3.305

98.757




4

3.159E-02

.632

99.389




5

3.056E-02

.611

100.000




 

El Cuadro Nş5.5 presenta las raíces características y su aporte en la varianza total explicada. Estas raíces constituyen a su vez las varianzas de las componentes, es decir :

Var Zh = m ´h V m h = l h

Donde V es la Matriz de correlaciones, por cuanto las variables están tipificadas. Adoptando como medida de variabilidad de las variables originales la suma de sus varianzas, la proporción de la componente h-esima en la variabilidad total será: : l h / Sl h o lo que es lo mismo: l h / p

Luego el vector de ponderaciones o pesos que se aplica a las variables originales para obtener la primera componente principal es el vector característico asociado a la raíz característica mayor de la matriz V.

El Cuadro N°5.6 presenta el primer vector característico, que constituye las ponderaciones que se tienen que aplicar a los datos estandarizados para hallar la primera componente principal.

CUADRO Nş5.6 COMPONENT SCORE COEFFICIENT MATRIX


Component
1

HVSA

.219

HVSAD

.210

HVSE

.220

HVCPT

.210

VCHAC

.200

Extraction Method: Principal Component Analysis.
Component Scores.

La Correlación entre las componentes principales y las variables originales es posible calcularlas mediante :

r jh = m h j ( l h ) ½

Ya que las variables originales están tipificadas.

La matriz factorial (factor matrix) esta dado por los coeficientes r j h representa la correlación entre la 1ra componente principal y las variables originales. Se presenta en el siguiente cuadro :

MATRIX FACTORIAL


Component
1

HVSA

.977

HVSAD

.934

HVSE

.981

HVCPT

.935

VCHAC

.890

Extraction Method: Principal Component Analysis.
a 1 components extracted.

 

Una vez calculados los coeficientes mh j se pueden obtener puntuaciones Z h i es decir, los valores de las componentes correspondientes a cada observación a partir de la siguiente relación..

Z h i = m h 1 X1i + m h 2 X2 i + …. + m h p X p i h= 1,2…p i= 1,2,…..n

Si una componente se divide por su desviación típica se obtiene una componente tipificada. Así, designando por Y h a la componente h-ésima tipificada, esta viene definida por :

Y h = Z h / ( l h ) ½ = m h 1 X1i / ( l h ) ½ + m h 2 X2 i / ( l h ) ½ +…. + m h p X p i / ( l h ) ½

Como ya se ha indicado, a la matriz formada por los coeficientes definidos mh 1 / ( l h ) ½ se le denomina matriz de puntuaciones de los factores, (factor score coefficient matriz)