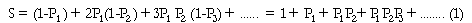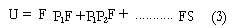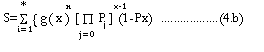|
A. Métodos alternativos para estimar la duración completa del desempleo. La data recogida directamente de las ENAHO (duración incompleta) no puede ser utilizada para el análisis de la duración del desempleo y es necesario estimar la duración completa del desempleo. Para esto existen hasta dos posibilidades: a. La estimación asumiendo estado estacionario. La primera forma de estimar la duración completa del desempleo es asumiendo que la economía se encuentra en estado estacionario32. Supongamos que cada semana un influjo de F personas ingresa a la situación de desempleo. De todos ellos, una proporción P1 continua desempleada en la segunda semana y (1-P1) deja el desempleo en esa semana. De los que continúan desempleados hasta la segunda semana (F*P1) una fracción P2 continua hasta la tercera semana y esto se prolonga hasta que todos los episodios de desempleo (spells) se han agotado. La proporción de desempleados que continúan en esa situación en la semana subsecuente (Pi) se conoce como la tasa agregada de continuación. La duración promedio completa de desempleo para las F personas que empezaron su desempleo en la misma semana es simplemente: Asumir que la economía se encuentra en
estado estacionario implica que los influjos son iguales en el tiempo (Fi=F) y que las tasas
de continuación son también constantes (Pi=P). En este caso, la duración
del desempleo (S) puede ser expresada como:
S = 1 / (1 - P) ...................(2)
Por lo tanto, el numero de desempleados totales (U) en cualquier punto del tiempo puede ser expresado como el producto del influjo semanal hacia el desempleo y la duración media del desempleo.
Esta es una relación bastante directa y atractiva desde el punto de vista de la intuición. El desempleo será alto si el flujo de ingreso al desempleo es alto o si la duración del desempleo es alta33. b. La estimación sin el supuesto de estado estacionario El supuesto de estado estacionario parece bastante restrictivo. Debido a ello algunos autores han propuesto algunos indicadores alternativos que intentan relajar este supuesto. El relajar este supuesto implica que el influjo de personas hacia el desempleo es variable (F i =F i(.)) y las tasas de continuación también (PX = F(x)/F(x-1)). En este caso, la ecuación (1) aún se aplica pero debe escribirse de la forma:
o más generalmente
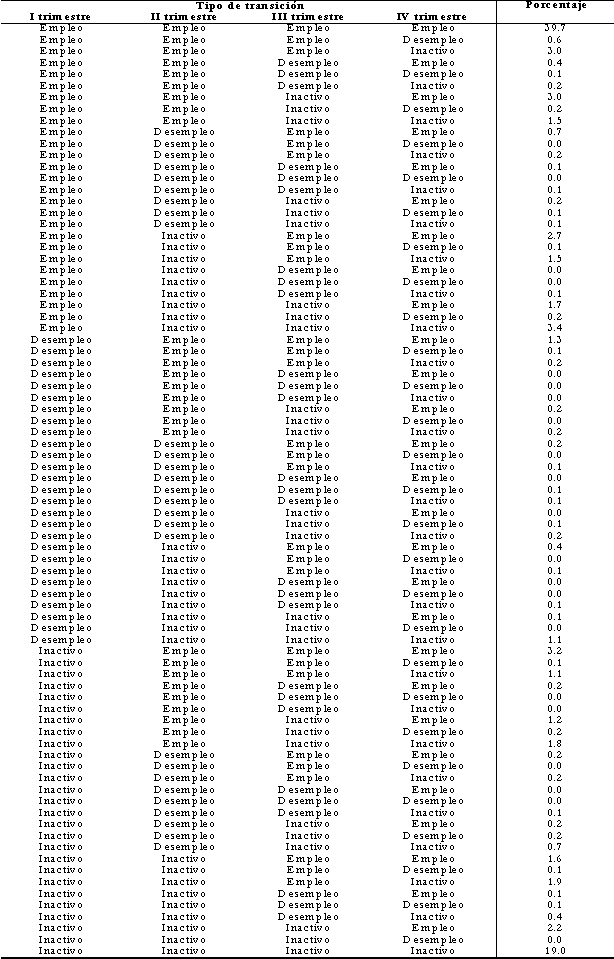
Aquí, P0 es la probabilidad de pertenecer al cohorte inicial y es igual a la unidad, el producto de los Pj y (1-Px) representa la fracción del cohorte inicial que sale del desempleo luego de x periodos, y la g(x) es una función que pondera a los individuos por la longitud de su episodio completo de desempleo. Para poder utilizar la expresión (4.b) es necesario conocer g(x). En este caso, Sider (1985) sugiere explorar la evidencia empírica. Si se sabe por ejemplo que los episodios de desempleo terminan en promedio en la mitad del periodo, entonces se podría pensar que g(1) = 0.5, g(2) = 1.5, etc. Sin embargo, el principal problema para poner en práctica este tipo de mediciones es usualmente el tipo de datos con que se cuenta para estimar los Pj . Existen dos grandes posibilidades : 1. Datos de panel. Cuando se cuenta con datos de tipo longitudinal (panel) es posible completar algunas duraciones de desempleo que usualmente se encuentran truncadas en las encuestas de cross section34. Asimismo, es posible estimar las tasas de continuación para los mismos individuos con mas precisión. En este caso se utilizan los siguientes elementos. Se requiere la probabilidad de salir de la fuerza de trabajo o encontrar empleo (PUI y PUE) para personas que han estado desempleadas diferentes periodos de tiempo. Luego se ajusta una curva que relaciona la duración con la probabilidad de salida del desempleo. Esto permite estimar la distribución de duraciones completas del desempleo. Se trabaja directamente con la función de riesgo que relaciona las probabilidades de salida con la duración, por tanto no se depende del supuesto del estado estacionario. 2. Datos de corte transversal. Por otro lado, dado que la existencia de paneles no es común, aun con encuestas continuas (tal vez mensuales) se pueden calcular tasas de continuación sin depender del supuesto de estado estacionario. En este caso se puede estimar P1t (la probabilidad en el periodo t de que un individuo desempleado en el primer periodo continúe en esa situación en el segundo periodo) como el número de personas en su segunda semana de desempleo en la semana t, como una proporción del número de personas en su primera semana de desempleo en la semana t-1. En este caso, P1t = h(1,t)/h(0,t-1) lo cual claramente contrasta con el caso del estado estacionario donde el cálculo sería P1t = h(1,t)/h(0,t). B. Perú Urbano: Transiciones en el mercado de trabajo al interior de 1996
Fuente: INEI. Panel 96. |
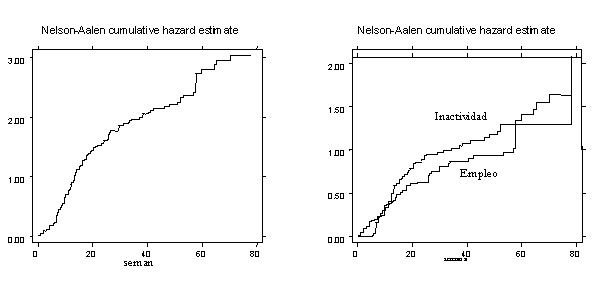
C. Gráficos
• Estimadores Kaplan-Meier para los Pobres, los Jóvenes, las Mujeres y los Cesantes
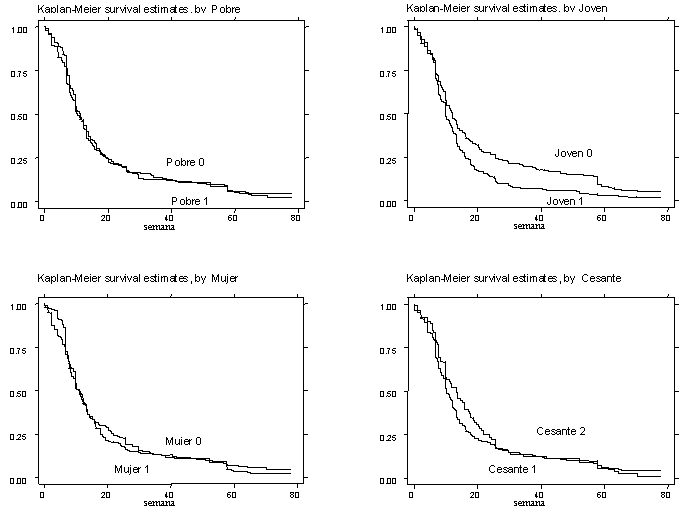
• Tasas de Riesgo integradas para grupos específicos
• Pobres (quintiles I y II)
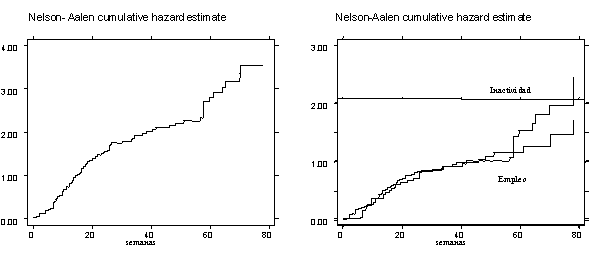
• Jóvenes (Menores de 25 años)
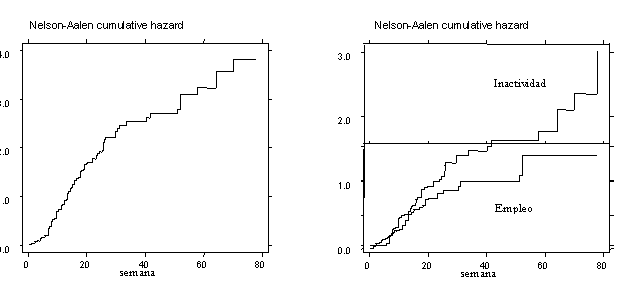
• Mujeres
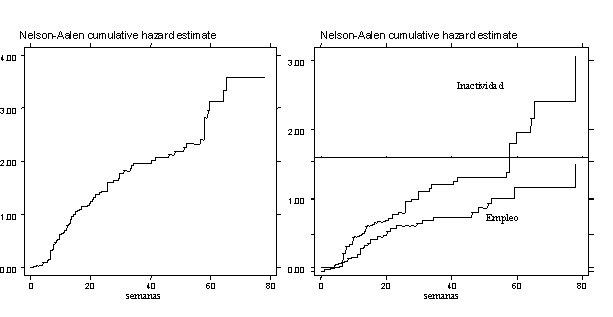
• Cesantes
D. Regresiones
Modelo Weibull: Riesgo total y dos riesgos 1996
Tasas de riesgo estimadas
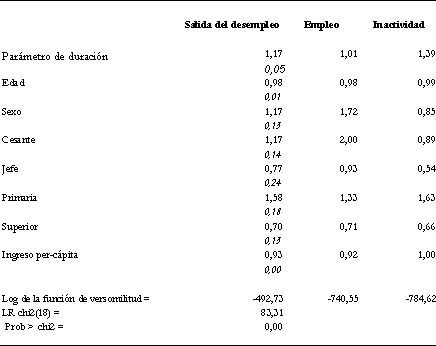
Nota: Los errores estándar de los parámetros de la regresión aparecen en cursiva.
Modelo Weibull: Riesgo total y dos riesgos 1996
Tasas temporales (Time rates) estimadas
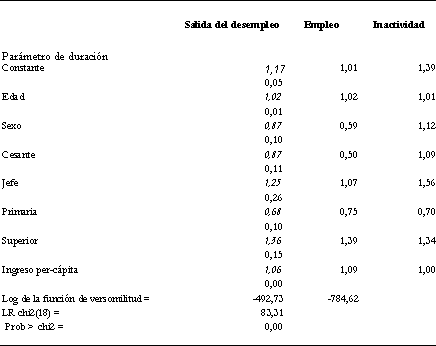
Nota: Los errores estándar de los parámetros de la regresión aparecen en cursiva.
E. Recomendaciones sobre las preguntas de las encuestas
Dado que el desempleo es un fenómeno fundamentalmente dinámico y por tanto es necesario tomar en cuenta esta característica tanto en el análisis como en el diseño de las encuestas. En un mercado cambiante, sería necesaria la incorporación de una estrategia operativa de recojo de datos con una perspectiva más amplia sobre el problema.
Así, para captar ese fenómeno se puede tomar una definición como la de PEA habitual con un año de período de referencia, a fin de percibir de manera más precisa todas las variantes de la dinámica del desempleo. Así, seria útil la incorporación de un módulo de preguntas sobre la situación laboral de las personas a lo largo del año (en la Encuesta Nacional de Hogares del III trimestre), tanto para identificar los patrones de cambio de la condición de actividad de las personas como el tipo de movilidad laboral (por lo menos a nivel de actividades económicas, y si fuera posible por grupos de ocupación)
Por otro lado, es también importante observar indicadores como la rotación laboral, el tiempo desempleado en el año, la duración del desempleo, de dónde proviene y cómo termina, entre otros, ya que estos ayudan a completar la visión del mercado laboral. En este sentido, sería conveniente incluir preguntas que permitan elaborar un balance tiempo en el año a fin de identificar, el tiempo sin empleo, tiempo desempleado y tiempo en el trabajo actual sobre todo en el caso de encuestas con componentes panel. Igualmente, para la identificación de las personas que entran al desempleo sería recomendable la inclusión en estas encuestas de la pregunta sobre el motivo por el cual la persona dejó de trabajar.
Dado que las principales transiciones observadas en el mercado de trabajo ocurren entre el empleo y la inactividad tal vez sea conveniente pensar en la posibilidad de incorporar en el caso peruano la metodología de encuestas continuas que cubran todo el año, lo cual permitiría tener una visión completa de todos los eventos que ocurren en el mercado de trabajo de manera permanente, el uso de indicadores como la PEA habitual. En particular, la incorporación de preguntas que permitan distinguir a los inactivos permanente de los temporales. La información de estas encuestas, y el uso de indicadores como la PEA habitual, permitiría identificar de que magnitud son las diferencias entre las personas que aparecen como desempleadas y los inactivos temporales detectando la posible presencia de pequeños periodos de inactividad (presumiblemente por desaliento) enmarcados dentro de un contexto de búsqueda de empleo.