|
|
5. Evaluación Estadística de los Modelos
5.1. Pruebas estadísticas
Para evaluar los modelos de regresión obtenidos se requiere realizar las siguientes pruebas estadísticas :
5.1.1 Prueba t de la Hipótesis nula de que el valor poblacional de cada coeficiente de regresión individual es cero, es verdadera.
Si algunos de los coeficientes (bi) del modelo fuesen nulos, significaría que las variables correspondientes no son importantes en la determinación del Ingreso. Por lo tanto, es sumamente importante determinar la validez de estos coeficientes, para ello se utilizan los estadísticos t que se presentan.
Adicionalmente, como se trata de muestras grandes, la distribución t se aproxima a la Normal y por tanto se utilizará esta distribución. A un nivel de significancia de 5%, se rechaza la hipótesis nula cuando el valor de la estadística t en valor absoluto sea mayor o igual a 1.96; concluyendo que el respectivo coeficiente de regresión es significativamente diferente de cero.
Con respecto a esta estadística, se resalta que como se puede observar en el informe, en las secciones 5.4 a 5.7 del Capítulo V, los valores de la estadística t para cada coeficiente en todos los modelos es mayor que 1.96, por lo tanto se concluye que cada coeficiente es significativamente diferente de cero.
5.1.2 Prueba de significancia global del modelo, que prueba la Hipótesis Nula que todos los parámetros del modelo excepto el intercepto son simultáneamente iguales a cero. Se estima el estadístico de la prueba que aproximadamente tiene una distribución F con grados de libertad: ?1 igual al número de parámetros a probar y ?2 igual al número de conglomerados menos el número de estratos de la muestra.
5.1.3 El coeficiente de determinación R2, que mide la proporción de variabilidad del Ingreso que es explicada mediante el Modelo de Regresión.
5.2. Análisis de los residuales
Este análisis se lleva a cabo para comprobar si se cumplen o no los supuestos del modelo.
En el Modelo de Regresión se supone que los errores verdaderos son independientes con distribución N (0,s2). Los residuos que se obtienen en el proceso son estimaciones de los verdaderos errores y la estimación de s2 es la media de los cuadrados de los residuos, s2 , donde s es el error estándar de la estimación.
El hecho que la media de los residuos sea igual a cero es consecuencia del método de estimación de los parámetros en la función de regresión.
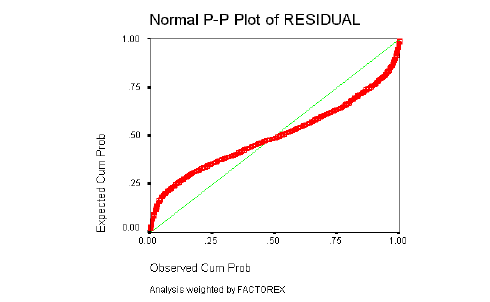
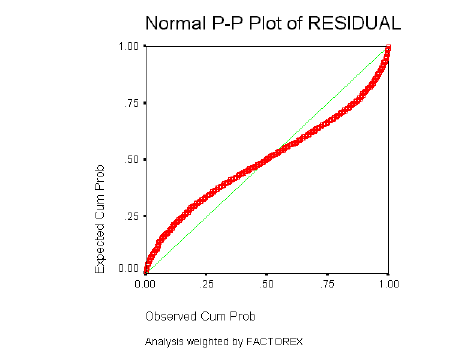
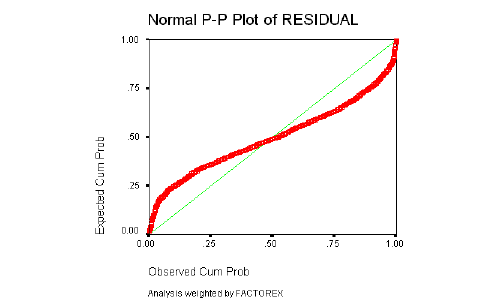
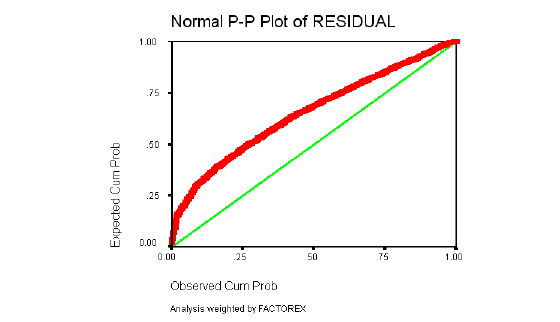
La Distribución de los residuos debe ser Normal: los residuos observados y esperados bajo la hipótesis de Distribución Normal deben ser parecidos. Esta suposición se comprueba con el gráfico de probabilidad Normal, que permite comparar gráficamente la función de distribución observada en la muestra tipificada, con la función de distribución Normal. Si la distribución de los residuos fuera Normal, dichos valores deberían ser aproximadamente iguales y en consecuencia, los puntos del gráfico estarían situados sobre la recta que pasa por el origen con pendiente igual a 1.
Respecto a la independencia, el valor observado en una variable para un individuo no debe ser influenciado en ningún sentido por los valores de esta variable observados en otros individuos: los residuos no deben presentar ningún patrón sistemático respecto a la secuencia de observación. El estadístico D de Durbin-Watson, mide el grado de autocorrelación entre el residuo correspondiente a cada observación y la anterior. Si el valor es próximo a 2, los residuos estarán incorrelacionados; si se aproxima a 4, estarán negativamente autocorrelacionados y si se aproxima a 0 estarán positivamente autocorrelacionados.
El estadístico D se calcula con la siguiente fórmula:
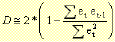
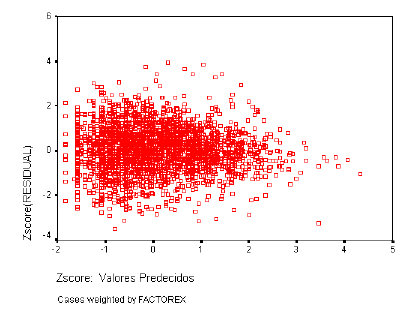
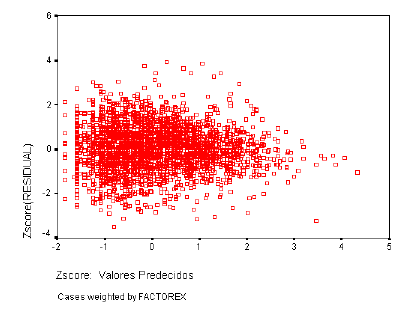
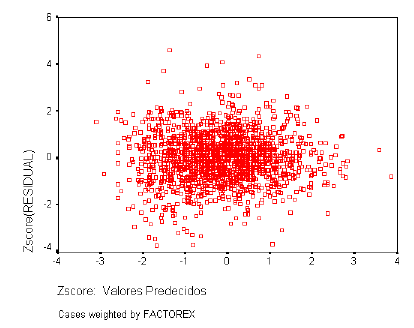
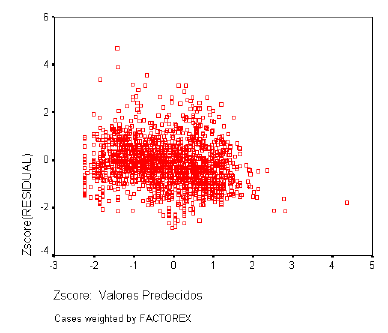
Las varianzas de las distribuciones de la variable dependiente ligadas a los distintos valores de las variables independientes deben ser iguales. Los residuos no deben presentar ningún patrón sistemático respecto a las predicciones o respecto a cada una de las variables independientes. Para analizar la homogeneidad de varianzas utilizaremos el gráfico de dispersión de los residuos tipificados frente a las estimaciones tipificadas.
En las secciones que siguen se presentan el gráfico de probabilidad Normal, el estadístico D de Durbin-Watson y el gráfico de dispersión de los residuos tipificados frente a las estimaciones tipificadas para cada uno de los Dominios.
5.3. Resumen de los Estadísticos para los Dominios de Estudio
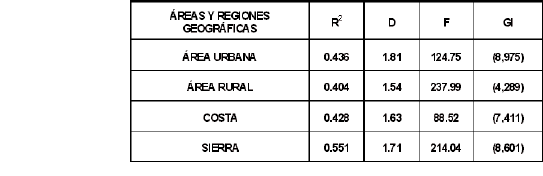
El presente cuadro, resume los resultados de Coeficiente de determinación R2, Estadística F, los grados de libertad en cada caso y la estadística D de Durbin-Watson.
Los coeficientes de determinación más altos son para Sierra Sur, Sierra Centro y Lima Metropolitana, dominios en los cuales los modelos de regresión obtenidos, explican más del 50% de la variabilidad de los ingresos de los hogares.

La estadística F, cuya hipótesis nula prueba la nulidad simultánea de todos los parámetros (excepto el intercepto) en los modelos, es rechazada, indicando validez en los modelos ajustados.
La estadística D de Durbin-Watson que prueba la independencia de los residuos, es decir, que valores observados en una variable para un individuo no deben verse influenciados por los valores de la variable en otros individuos, proporciona valores que pueden fluctuar entre 0 y 4. Un valor cercano a cero indicará autocorrelación positiva, en tanto que uno cercano a 4, autocorrelación negativa. El valor 2 indica ausencia de autocorrelación; que es lo esperado en un modelo de Regresión. Como se observa en los ocho dominios en estudio, todos los valores son relativamente cercanos a 2; siéndolo exactamente igual en la Costa Centro.
Además de la independencia de los residuos, para ayudar a determinar la validez del modelo, interesa conocer si los residuos tienen distribución normal con media cero y, determinar la homogeneidad de las varianzas.
Normalidad y homocedasticidad de los residuos
La normalidad de los residuos se determinará a través de los gráficos de probabilidad Normal, en los que se describe el comportamiento de los residuos al estimar el modelo y contrastarlo con los datos originales.
Como ya se ha descrito con detalle, el resultado debe ser similar al de una recta que pasa por el origen, si el gráfico se asemeja a una recta, los errores tienen una distribución Normal, si el gráfico resultante sigue otro patrón o está concentrado en torno a un punto determinado (nube de puntos); no se puede decir que los residuales del modelo tengan una Distribución Normal.
A continuación los gráficos de normalidad de residuos y homogeneidad de varianzas para cada dominio.
5.3.1 LIMA METROPOLITANA
Normalidad de los Residuos


5.3.2 COSTA NORTE
Normalidad de los Residuos
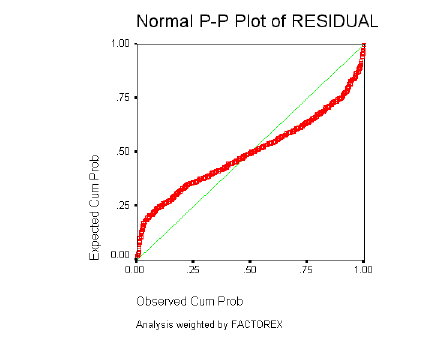

5.3.3 COSTA CENTRO
Normalidad de los Residuos

Homogeneidad de Varianzas
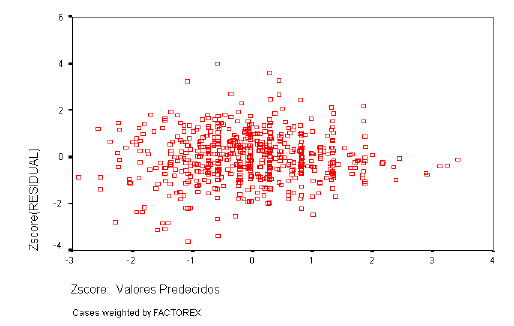
5.3.4 COSTA SUR
Normalidad de los Residuos
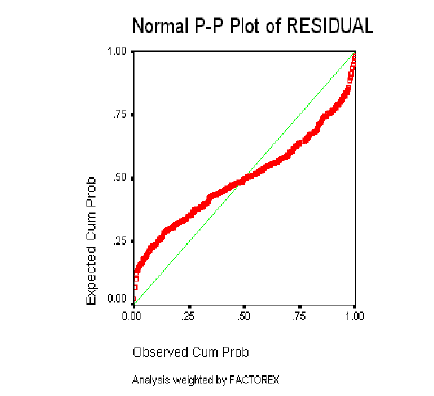
Homogeneidad de Varianzas
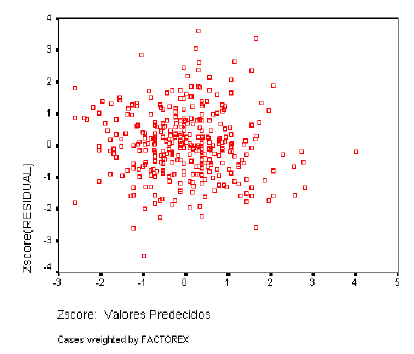
5.3.5 SIERRA NORTE
Normalidad de los Residuos
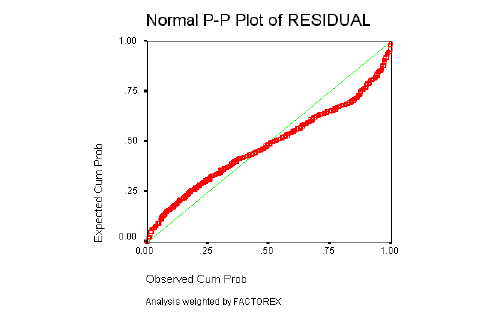
Homogeneidad de Varianzas

5.3.6 SIERRA CENTRO
Normalidad de los Residuos

Homogeneidad de Varianzas

5.3.7 SIERRA SUR
Normalidad de los Residuos
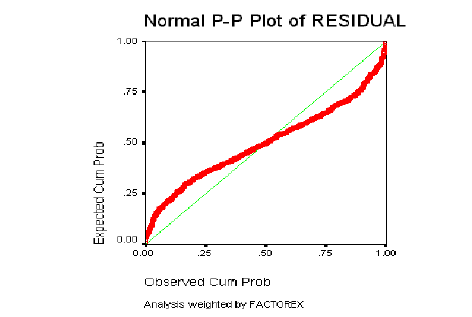
Homogeneidad de Varianzas
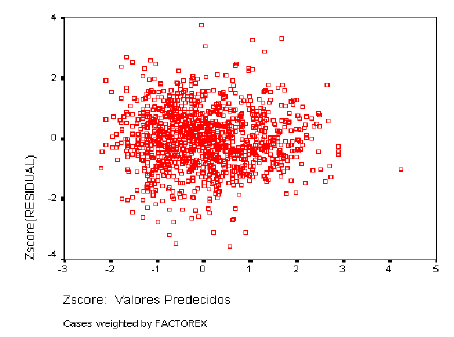
5.3.8 SELVA
Normalidad de los Residuos

Homogeneidad de Varianzas

Resumiendo las pruebas estadísticas realizadas en cada uno de los Dominios, se evidencia que cada uno de los coeficientes de regresión es estadísticamente diferente de cero, asimismo se comprueba la validez de los Modelos de Regresión Ajustados.
De los resultados del análisis de los residuales se tiene:
Los coeficientes de determinación obtenidos son bajos, varían entre 0.37 y 0.60, pero considerando que los aspectos analizados son satisfactorios podemos considerar que por lo menos los modelos de Lima Metropolitana (R2 = 0.533), Sierra Centro (R2 = 0.574) y Sierra Sur (R2 = 0.604) tienen un buen ajuste y pueden utilizarse con confianza; los otros deben utilizarse con reserva. Cabe también anotar que las aproximaciones anotadas en el análisis de los residuales son mejores para estos tres Dominios.
Por otra parte es interesante anotar que un R2 alto puede indicar la presencia de multicolinealidad entre las variables explicativas, que no es el caso.
5.4. Resumen de los Estadísticos para los Estratos de Ingresos
El presente cuadro, resume los resultados de Coeficiente de determinación R2, Estadística F, los grados de libertad en cada caso y la estadística D de Durbin-Watson.
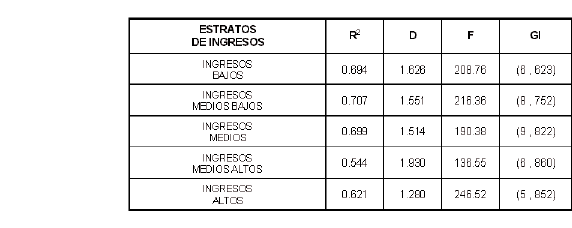
En general, los coeficientes de determinación para los Quintiles de ingreso, son más altos que los obtenidos en los ocho dominios geográficos. Los más altos son para el segmento de ingresos Medio Bajos, Ingresos Medios e Ingresos Bajos, estratos en los cuales los modelos de regresión obtenidos, explican alrededor del 70% de la variabilidad de los ingresos de los hogares.
La estadística F, cuya hipótesis nula prueba la nulidad simultánea de todos los parámetros (excepto el intercepto) en los modelos, es rechazada, indicando validez en los modelos ajustados.
La estadística D de Durbin-Watson que prueba la independencia de los residuos, según lo observado en los quintiles de ingreso, en cuatro de los cinco segmentos es relativamente cercana a 2, en el segmento de Ingresos Altos, se acerca a 1, lo que cierta autocorrelación positiva de las variables.
Además de la independencia de los residuos, para ayudar a determinar la validez del modelo, interesa conocer si los residuos tienen distribución normal con media cero y determinar la homogeneidad de las varianzas. A continuación se presentan las respectivas pruebas gráficas para cada uno de los Estratos de Ingresos.
5.4.1. ESTRATOS DE INGRESOS BAJOS
Normalidad de los Residuos
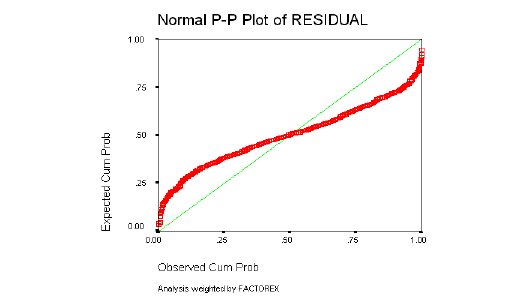
Homogeneidad de Varianzas

5.4.2 ESTRATOS DE INGRESOS MEDIOS BAJOS Normalidad de los Residuos
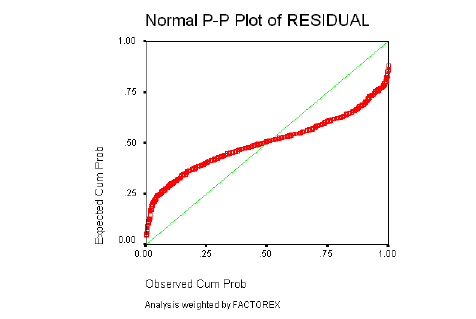
Homogeneidad de Varianzas

5.4.3 ESTRATOS DE INGRESOS MEDIOS Normalidad de los Residuos
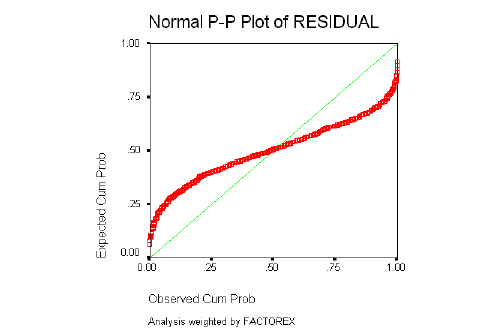
Homogeneidad de Varianzas
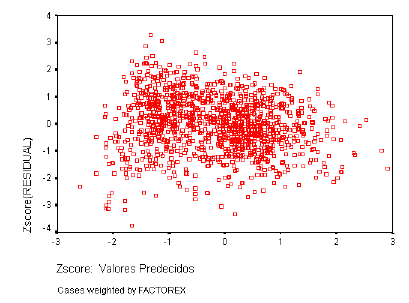
5.4.4 ESTRATOS DE INGRESOS MEDIOS ALTOS Normalidad de los Residuos
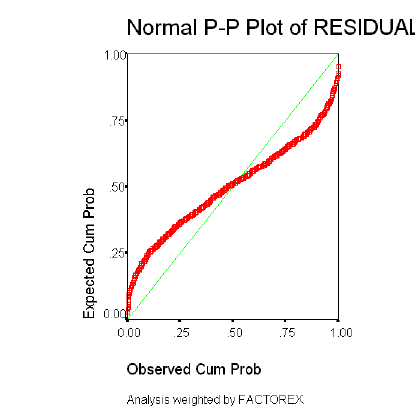
Homogeneidad de Varianzas
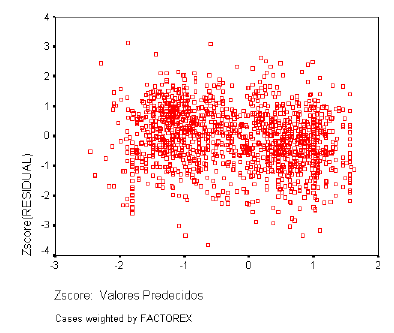
5.4.5 ESTRATOS DE INGRESOS ALTOS Normalidad de los Residuos
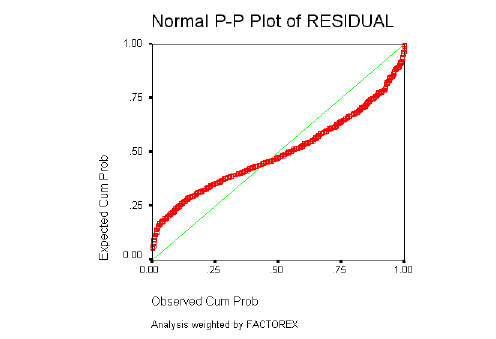
Homogeneidad de Varianzas
De los resultados del análisis de los residuales se tiene:
|