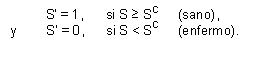3.3.1. El indicador de salud

La literatura económica reconoce a la salud como una variable no observable, que puede ser sólo aproximada por indicadores siempre imperfectos. En este contexto, se ha ensayado el empleo de medidas antropométricas de talla y/o peso (p. ej., Rosenzweig y Schultz, 1983; Rosenzweig y Wolpin, 1986; Barrera, 1990; Pitt, Rosenzweig y Hassan, 1990; Schultz, 1996) y los reportes personales de enfermedad o incapacidad (p. ej., Wolfe y Behrman, 1984; Pitt y Rosenzweig, 1985; Schultz, 1997; Cortez 1999). A nivel más agregado, se han utilizado valores promedios de las variables anteriores y, también, las tasas de mortalidad o de supervivencia (Rosenzweig y Schultz, 1982; Pitt, Rosenzweig y Gibbons, 1995) Recientemente Knaul (1999) utilizó el reporte de la edad de la primera mestruación (age at menarche) como indicador de la salud y nutrición de las mujeres de México.

Formalmente, el problema de medición plantea una diferencia k entre la salud real y el indicador empleado S':

k = S' - S Þ S' = S + k.

Este error de medición k implica que, al estimar la ecuación de salud (3.2), el uso de S' como variable dependiente incluye en el error eS al verdadero error (jS) y, también, al error k. Además, se considera que las "dotaciones" no observadas (mS) son capturadas por el error, de modo que

E_S = Q_S + k + U_S'

Si el error de medición se hallase sistemáticamente relacionado con otras variables explicativas de la salud (XS), se distorsionarían las estimaciones de los impactos de las mismas. Considerando ,

eS = jS + k + mS, la correlación es más probable. Por ejemplo, los errores de medición pueden causar las distorsiones anteriores cuando la información del estado de la salud proviene de reportes de los propios individuos. La percepción de la propia salud y, por tanto, el error de medición k (y eS) estaría correlacionados con ciertas características personales.

Así, personas con mayor educación o con mayor acceso a los servicios de salud tendrían una mayor probabilidad de detectar y reportar síntomas de enfermedad. En la estimación de (3.2), se apreciaría entonces un sesgo hacia abajo del coeficiente de la educación o de la atención médica2. De hecho, la relación entre los cuartiles de ingreso y el verdadero estado de salud podría ser más fuerte que la observada en el Cuadro 1.

donde S' es el indicador dicotómico de salud y SC es un cierto nivel crítico de fortaleza del estado de salud. Por debajo de SC, el individuo cae enfermo. A su vez, el indicador S', siendo dicotómico, requiere un modelo de regresión probit de estimación.

Más allá de los efectos explícitos entre salud y productividad, recogidos en las ecuaciones (3.1) y (3.2), la teoría explica que también la correlación de los términos de error de esas ecuaciones causa relaciones de simultaneidad. En la medida que eW y eS denotan los errores de las ecuaciones de salario y de salud, habría un problema de simultaneidad si Cov(eW, eS) fuese distinta de cero.

Según se ha discutido en la sección anterior, puede escribirse eS = jS + k + mS y eW = jW + mW. De este modo, aun cuando los verdaderos errores jW y jS se distribuyen independientemente, se tendría Cov (eW, eS) = Cov (mW, mS), probablemente distinta de cero.

En primer lugar, la relación entre mW y mS podría basarse en que una misma característica personal facilita una mayor productividad y, a la vez, permite conservar un mejor estado de salud (cierta habilidad peculiar o capacidad física, o algún rasgo psicológico). En segunda instancia, tal relación puede apoyarse también en la conducta de los agentes. Por ejemplo, una alta dotación en favor de la productividad (mW) genera un incentivo a invertir en reforzarla (o en compensarla dentro de la unidad familiar) a través de variables no observables recogidas en mS (cierta preocupación especial por promover la salud, por ejemplo).

La simultaneidad discutida entre salario y salud, así como el error de medición, conduce al empleo de métodos bietápicos de estimación. En la primera etapa, la salud es predecida con variables sólo exógenas y, entre ellas, aquellas que explican al salario. Las predicciones de esta regresión serían empleadas luego como indicador de salud en la regresión salarial. De este modo, inicialmente,

donde el conjunto XW juega el papel de W y, por tanto, esta primera regresión auxiliar se asemeja a (3.2). Al estimar los impactos de XW, P y XS sobre la salud S, permite luego predecir valores SIV que, libres del error de medición k y de las dotaciones mS, constituyen indicador no simultáneo a W, mejor que el S' original.

En la segunda etapa, las predicciones SIV se incluirían en la ecuación salarial:

Donde se emplea una especificación semilogarítmica utilizada por la mayor parte de los estudios empíricos que calculan los retornos del capital humano.

La ecuación de salarios (4.2) presenta el conocido sesgo de selección que puede arrojar estimados sesgados de no utilizar el procedimiento de estimación en dos etapas sugerido por Heckman (1978) y Lee (1983). La ecuación dicotómica que determina la decisión de participación en el mercado laboral (J) incluye como variables explicativas el salario, la salud y, además, un conjunto de variables XJ, que identifica el sistema. En la estimación, el salario no se incluye directamente porque no se observa cuando el individuo no participa en el mercado laboral (J=0), de modo que es reemplazado por sus variables explicativas XW.

El conjunto de ecuaciones (4.1), (4.2) y (4.3) forma el sistema de ecuaciones por estimar. Con los resultados de la ecuación (4.3) se genera el corrector de selectividad que es incluido en la ecuación salarial (4.2). En el inicio, la ecuación (4.1) ofrece un índice de salud SIV más preciso que el uso de la no ocurrencia de enfermedad S', que sólo refleja si S es mayor o menor que SC. A su vez, SIV puede interpretarse como la probabilidad de permanecer sano durante tres meses.