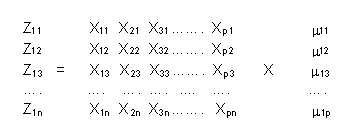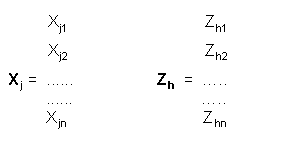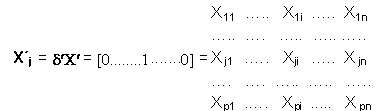|
Una de las primeras actividades realizadas en el desarrollo de la investigación fue la selección de indicadores que expliquen los niveles de vida alcanzados por una población en un ámbito determinado. Como es lógico, tuvimos en primer lugar las restricciones que impone la información disponible. La información sobre los niveles de vida ha sido tomada de la encuesta ENAHO realizada durante el cuarto trimestre de 1998. La información de base para el análisis del año 1993, fue tomada de una muestra del 5% del Censo de Población y Vivienda. Dicha muestra fue seleccionada por el INEI y los resultados alcanzados se acercan con un pequeño margen de error al obtenido a través del Censo. La unidad de análisis considerada en ambas encuestas fue el Hogar. Sin embargo para fines del estudio, se consideró necesario analizar el nivel de vida alcanzado por los hogares en un ámbito geográfico determinado. En este sentido la restricción la puso la Encuesta ENAHO ya que con base a sus características se puede inferir a 8 dominios: Costa Norte, Costa Centro (excepto Lima Metropolitana), Costa Sur, Sierra Norte, Sierra Centro, Sierra Sur, Selva y Lima Metropolitana. Con la limitación que imponen la ENAHO y el CPV 93, se seleccionaron indicadores que puedan ser calculados en base a ellas y se calculó su valor en cada uno de las ámbitos de inferencia de la ENAHO 98-IV. A partir de los indicadores simples y su análisis descriptivo, se empleó el análisis multivariado, para calcular los indicadores parciales y el indicador sintético global. Posteriormente se analizaron los resultados. Dado que importantes indicadores considerados en las ENAHO IV de 1997 y 1998 (entre ellos el ingreso y el gasto) no se consideraron en el CPV, se empleó la misma metodología para evaluar la evolución los niveles de vida en dicho periodo. Los resultados se presentaron en el informe parcial. En este caso, los niveles de inferencia considerados, fueron Costa Urbana, Costa Rural, Sierra Urbana, Sierra Rural, Selva, Lima Metropolitana y el Nivel nacional. Los resultados se adjuntan. Los resultados pusieron a prueba la metodología para construir indicadores sintéticos con capacidad de realizar comparaciones interespaciales e intertemporales. La mayoria de los indicadores utilizados fueron incluidos en el Informe Final. Descripción Teórica del Método La utilidad principal del análisis de componentes principales reside, en que permite estudiar un fenómeno multidimensional, cuando algunas o muchas de las variables comprendidas en el estudio están correlacionadas entre si, en mayor o menor grado. En realidad, al estudiar un fenómeno multivariable, las correlaciones entre las variables que explican el fenómeno, se constituyen en un "velo" que impide evaluar adecuadamente el papel que juega cada variable en el fenómeno. El Análisis de Componentes Principales tiene como objetivo el hallar combinaciones lineales de variables representativas de cierto fenómeno multidimensional, con la propiedad de que exhiban varianza máxima y que a la vez estén incorrelacionadas entre si. La varianza de la componente es una expresión de la cantidad de información que lleva incorporada. Es decir cuanto mayor sea su varianza, mayor será la cantidad de información incorporada en dicha componente. Por ésta razón las sucesivas combinaciones o variantes o componentes se ordenan en forma descendente de acuerdo a la proporción de la varianza total presente en el problema, que cada una de ellas explica. La primer componente es por lo tanto, la combinación de máxima varianza; la segunda es otra combinación de variables originarias que obedece a la restricción de ser ortogonal a la primera y de máxima varianza, la tercer componente es aún otra combinación de máxima varianza, con la propiedad de ser ortogonal a las dos primeras; ..... y así sucesivamente Por sus propiedades de ortogonalidad, las sucesivas componentes después de la primera se pueden interpretar como las combinaciones lineales de las variables originarias que mayor varianza residual explican, después que el efecto de las precedentes ha sido ya removido y así sucesivamente hasta que el total de varianza ha sido explicado. Es posible que unas pocas primeras componentes logren explicar una alta proporción de la varianza total; en este caso que ocurre cuando las variables están correlacionadas en mayor grado, las componentes pueden sintéticamente sustituir a las múltiples variables originarias. Ello permitiría resumir en unas pocas variantes o componentes no correlacionadas gran parte de la información originaria. Desde este punto de vista, el método de componentes principales es considerado como un método de reducción, ya que puede reducir la dimensión del numero de variables que inicialmente se han considerado en el análisis. a) Obtención de las componentes principales En primer lugar, es necesario indicar que la obtención de componentes principales es un caso típico de cálculo de raíces y vectores característicos de una matriz simétrica. Esta matriz simétrica es la conformada por la matriz de correlaciones de las variables consideradas en el estudio del fenómeno multidimensional. i) Obtención de la primera componente Consideremos que disponemos de una muestra de n observaciones sobre el comportamiento de p variables X1, X2, X 3 …. Xp que explican un fenómeno multidimensional. Estas variables deben de estar expresadas en desviaciones respecto a la media o en variables tipificadas. La primera componente al igual que las siguientes, se expresa como combinación lineal de las variables originales, es decir: Z1i = m11 X1i + m12 X2i + ................. m1p Xp1Donde Z1i es el valor de la componente Z1 para la observación i. Asimismo, X1i X2i X3i son los valores de las variables X1, X2 , X3 , en la observación i. Finalmente m11, m 12, m13, … m1p es el vector de pesos o coeficientes cuyo valor queremos determinar.Para el conjunto de las n observaciones muestrales esta ecuación se puede expresar matricialmente de la siguiente forma:
Si la expresamos en forma vectorial tenemos: Z1 = X m 1La primera componente es obtenida de forma que su varianza sea máxima, sujeta a la restricción de que la suma de los pesos (m1j) al cuadrado, sea igual a la unidad. La varianza de la primera componente, dada por: Var (Z1) = (
S Z21i ) / n = ( z´1 z1 ) / n = (
m ´1 X´ X m
1 ) / n = m
´1 ( X´ X) / n m
1
ya que la media de las Z1 es igual a 0 debido a que las X j variables
están expresadas en desviaciones con respecto a la media o están tipificadas. Si las variables están expresadas en desviaciones respecto a la media ( 1/n)
X´X es la matriz de covarianza de las Xj variables. Si las variables están tipificadas (1/n)
X´X es igual a la matriz de correlaciones. Si denominamos a la matriz X´X como V, la varianza de la primera
componente seria : Var (Z1) =
Si queremos que Z1 tenga la máxima varianza tenemos que poner una restricción por que sino la varianza podría ser infinita. La restricción es que la suma de cuadrados de los coeficientes sea 1. S m 21i = m ´1 m 1 = 1Si incorporamos la restricción podemos formar el siguiente langragiano L = m ´1V m 1 - l ( m ´1 m 1 - 1 ) Para maximizar el valor del lagrangiano derivamos respecto a u1 e igualamos a 0: ¶ L / ¶ u1 = 2Vm 1 - 2l m 1 = 0es decir : (V - l I ) m 1 = 0 Al resolver la ecuación ½ V - l I ½ = 0 , se obtienen p raíces características. Si toma la raíz característica mayor ( l1) , se puede hallar el vector característico asociado aplicando : m ´1 m1 = 1. Luego el vector de ponderaciones o pesos que se aplica a las variables originales para obtener la primera componente principal es el vector característico asociado a la raíz característica mayor de la matriz V.ii) Obtención de las restantes componentes La segunda y las demás componentes Z h expresada en forma genérica y matricial será :Z h = X mhPara su obtención, además de la restricción de que : m´ m h = 1, se imponen restricciones adicionales para asegurar que la componente h-esima sea ortogonal a todos los vectores característicos calculados previamente.m h m1 = mh m2 = m h m3= ....... m h mh-1 = 0En resumen las p componentes principales que se pueden calcular son una combinación lineal de las variables originales, en las que los coeficientes de ponderación son los correspondientes vectores característicos asociados a la matriz V. Las varianzas de los componentes vienen dadas por las raices características es decir : Var Zh = m´h V mh = l h Adoptando como medida de variabilidad de las variables originales, la suma de sus varianzas, la prop. de la componente h-esima en la variabilidad total será: l h / Sl hEn el caso de variables tipificadas, como la matriz de covarianzas es la matriz de correlaciones, la prop. de la componente h-esima en la variabilidad total será: l h / pb) Correlación entre las componentes principales y las variables originales La covarianza entre la variable X j y la el componente Zh .Definamos los vectores muestrales de la componente Z h y la variable X j por :
La covarianza muestral entre X j y Z h viene dada por :Cov ( X j, Z h ) = ( X´ j Z h ) / nEl vector X j se puede expresar en términos de la matriz X, utilizando un vector de orden p, al que designaremos por d, que tiene 1 en la posición j-ésima y 0 en las posiciones restantes: Así
Luego, la Cov ( X j , Z h ) en términos de X y de d seráCov ( X j, Z h ) = ( d ¢C ¢ C m h ) / n = (d ¢ V m h ) / n = d ´l h m h = l h d ´m h = l h m h jLuego la correlación existente entre la variable X j y la componente Z h es la siguiente:r jh = Cov (X j, Zh) / (Var Xj Var Zh) ½ = l h m h j / (Var Xj l h ) ½Si las variables originales están tipificadas : rjh = m h j ( l h ) ½La matriz factorial (factor matrix) esta dado por los coeficientes r j hc) Puntuaciones sin tipificar y tipificadas Una vez calculados los coeficientes m h j se pueden obtener puntuacionesZ h i es decir, los valores de las componentes correspondientes a cada observación a partir de la siguiente relación..Z h i = m h 1 X1i + m h 2 X2 i + …. + m h p X p i h= 1,2…p i= 1,2,…..nSi una componente se divide por su desviación típica se obtiene una componente tipificada. Así, designando por Y h a la componente h-ésima tipificada, esta viene definida por : Y h = Z h / ( l h ) ½ = m h 1 X1i / ( l h ) ½ + m h 2 X2 i / ( l h ) ½ +…. + m h p X p i / ( l h ) ½ Como ya se ha indicado a la matriz formada por los coeficientes m h 1 / ( lh ) ½ se le denomina matriz de puntuaciones de los factores, (factor score coefficient matriz) En resumen se pueden obtener las siguientes conclusiones: 1) Las componentes principales son combinaciones lineales de las variables originales. 2) Los coeficientes de las combinaciones lineales son los elementos de los vectores característicos asociados a la matriz de covarianza de las variables originales . 3) La primera componente principal está asociada a la mayor raíz característica de la matriz de covarianzas de las variables originales. 4) La varianza de cada componente es igual a la raíz característica a que va asociada. 5) En el caso de que las variables estén tipificadas, la proporción de la variabilidad total de las variables originales captada por una componente es igual a la raíz característica correspondiente dividida por el número de variables originales. 6) La correlación entre una componente y una variable original se determina con la raíz característica de la componente y el correspondiente elemento del vector característico asociado, en el caso de que las variables originales estén tipificadas. d) Número de componentes a retener Uno de los objetivos de los Componentes principales es reducir las dimensiones del problema pasando de p variables originales a m compnentes principales siendo m < p Pero, cuantas componentes retener ? Una primera aproximación es el criterio de la media aritmética. Teniendo en consideración que la raíz característica de una componente es precisamente su varianza, se retiene a todas aquellas lh mayores que l promedio. En el caso particular de que las variables originales se encuentren tipificadas se selecciona aquellas componentes cuya raíz característica es mayor que 1. Es decir l h >1 e) Prueba de Hipótesis de las raíces características no retenidas Bajo el supuesto de que las variables originales siguen una distribución normal multivariante, se pueden formular las siguientes hipótesis relativas a las características poblacionales no retenidas: Ho : l m+1 = l m+2 = l m+3 = l m+4 …….. = l p = 0 Esta prueba se deriva de la prueba de esfericidad de Barlet y es el estadístico Q* = ( n - (2p+1) / 6 ) ( (p-m) ln l p-m - S ln l j ) Sigue una distribución Chi cuadrado con (p-m+2) (p-m+1) / 2 grados de libertad. Si Q* > X2 con (p-m+2) (p-m+1) / 2 grados de libertad se rechaza la hipótesis nula y prueba que una o mas de las raíces no retenidas son significativamente distintas de 0. |