Desde hace varios años se han propuesto procedimientos para estimar la cobertura del registro de defunciones, apoyándose en algunas relaciones fundamentales de las poblaciones estables. Brass propuso el método de la Ecuación del Equilibrio orientado a estimar una tasa media anual de crecimiento natural, un factor de corrección de las defunciones y una tasa bruta de mortalidad.
El método puede aplicarse a todas las defunciones o restringirse a partir de cierta edad en adelante. La información requerida consiste en defunciones por grupos de edad y la distribución de la población por edad. No es necesario que las defunciones y la población pertenezcan a u n mismo momento, pero sí a periodos cercanos.1
Brass propone el método para estimar la cobertura de las defunciones a partir de la ecuación fundamental:
N(x)/N(x +) = r + D*(x +)/N(x +)
Donde:
N(x), es el número de personas de edad exacta x.
N(x +), el número total de personas de x y más años.
D*(x +), el número total de defunciones que se producen en personas de x y más años.
r, la tasa de crecimiento.
En una población ideal, la representación gráfica de esta ecuación sería una línea recta con un ángulo de 45 grados que interceptaría al aje de las coordenadas a la altura de r. En una población real se observa frecuentemente que solamente parte de los puntos están alineados.
Bajo el supuesto que la estructura de las defunciones sea verdadera es razonable aceptar que se de una constancia en la proporción de omisiones con relación a las defunciones registradas, es decir:
D(x +) = f. D* (x +)
Donde:
D(x +), son las defunciones verdaderas de edad mayor a "x"
D*(x +), son las defunciones registradas de edad mayor a "x."
"f", es el factor de corrección de las defunciones registradas a edades mayores
a "x".
La aplicación al caso de la población de la ENAHO 98-2, la ecuación sería:
N (x)/N(x +) =r + f D*(x +)/N(x +)
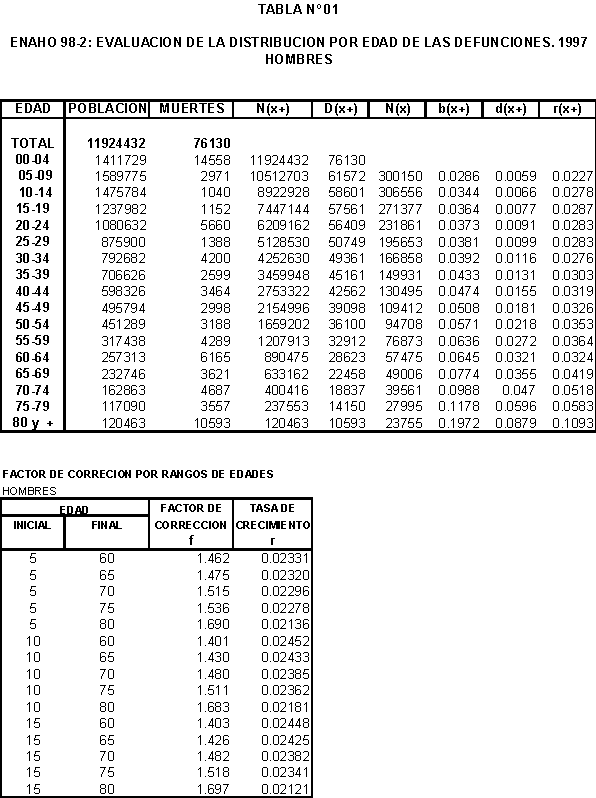
Las siguientes tablas ilustran el procedimiento.