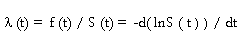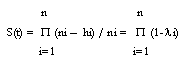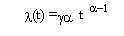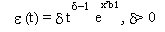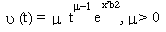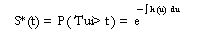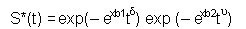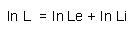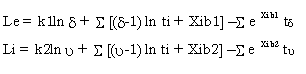|
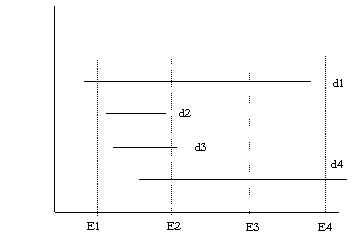
El análisis de la duración del desempleo es importante por diversas razones. Probablemente la más importante de ellas es que el bienestar de los individuos desempleados está ciertamente más relacionado al tiempo que ellos permanecen en esa condición que el mismo hecho de estar desempleados. En ese sentido, la tasa de desempleo sería un indicador menos útil que la duración del desempleo. En el presente capítulo se analiza detalladamente la distribución de la duración completa del desempleo en el Perú Urbano, utilizando para ello información proveniente del panel formado por la unión de las cuatro encuestas ENAHO de 1996 que ejecuta trimestralmente el INEI. • Los datosLos datos para el análisis de la duración del desempleo provienen de las Encuestas Nacionales de Hogares para el ámbito nacional urbano. En estas encuestas se recolecta información sobre duración del desempleo sólo para individuos desempleados en el momento de las encuestas razón por la cual esta información se encuentra incompleta o censurada. Para tener una idea más precisa de este punto se puede observar el Gráfico 5. Gráfico 4.2 La encuesta se realiza en cuatro trimestres en
el año. Supongamos simplificadamente que la fecha exacta de la encuesta ocurre en
Ei , (i=1,2,3,4). En cada E se pueden presentar diferentes sesgos. Por ejemplo, la
duración del desempleo del individuo 1 (d1) se captura en los tres primeros
trimestres hasta que deja de estar desempleado en el cuarto. Si solo se contara con
información de la primera encuesta, se tendría la impresión que la
duración del desempleo de este individuo es muy corta. Por otro lado, en d2 el caso
es más complejo. Dada la muy breve duración del desempleo (entre ambas encuestas)
este periodo de desempleo no se puede registrar en las encuestas y solo un análisis
de la duración del empleo o la inactividad permitiría identificarla plenamente.
En d3 la duración del desempleo se captura en la encuesta E2 y si solo se tuviera
información de esta encuesta daría la impresión que la duración
fuera mas larga. En d4, la data recogida directamente de las ENAHO claramente no permiten
conocer todo el episodio de desempleo y por esta razón, es necesario estimar la
duración completa del desempleo.
Los datos utilizados para realizar estas estimaciones son de tipo panel.
La naturaleza de los datos disponibles (panel con información de los 4 trimestres de
1996 y panel con las encuestas 1997-IV y 1998-IV) determinan el método de
estimación a utilizarse. Existen dos características particulares que es
necesario tomar en cuenta. Por un lado, dado que se cuenta con información de tipo
panel se pueden completar algunos episodios de desempleo, en particular para individuos cuyo
desempleo terminó en empleo, dado que en la segunda observación se cuenta con
la pregunta de duración del empleo. En el caso de aquellos individuos cuyo episodio
de desempleo continúa hasta la ultima observación o termina en inactividad, no
se puede completar los episodios de desempleo y por tanto dichas observaciones se encuentran
censoradas hacia la derecha. En estos casos es necesario realizar una estimación de
la duración esperada del desempleo. Por otro lado, dado que las ENAHO se aplican a
lo largo de un trimestre en diferentes segmentos de la muestra no se puede asumir que todos
los episodios de desempleo empiezan en la misma fecha. Por tanto es necesario controlar por
la fecha de ingreso a la condición de desempleo de los individuos a la hora de
realizar las estimaciones23. • Como se ha mencionado la información
que recogen las encuestas de hogares se refiere a la duración del desempleo hasta la
fecha de la entrevista, lo cual quiere decir que se trata de la duración incompleta
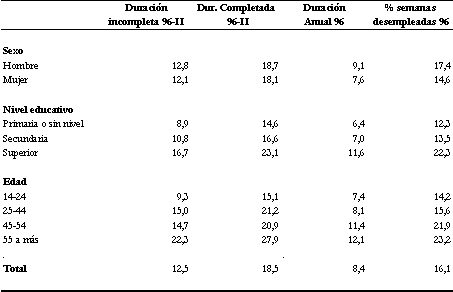
del desempleo. Según los datos observados el promedio de la duración
incompleta en el segundo trimestre de 1996 ascendió a 12.5 semanas es decir a unos
tres meses.
Sin embargo, cuando se completan estas duraciones con informacion de los
paneles24, se encuentra que la duracion promedio sube a 18.5 semanas, es decir,
unos 4 meses y medio. Un aspecto notable del indicador de duración es que muestra un
comportamiento diferente a la tasa de desempleo cuando se desagrega por sub-grupos. Las
mujeres exhiben promedios de duración prácticamente iguales a los de los
hombres, los periodos de desempleo se incrementan a medida que crece la edad y más
importante aún, los promedios de desempleo crecen a medida que se alcanza mayor nivel
educativo.
Cuadro 4.3 Fuente: Panel 96. INEI. Es interesante notar que los promedios de duración completa e
incompleta mencionados anteriormente recogen toda la experiencia histórica de
desempleo acumulada por los individuos sin referencia a un periodo de tiempo. En ese sentido,
un indicador indicativo y complementario sobre el desempleo sería el número de
semanas desempleadas existentes en el país al año. Las estimaciones en base a
la información sobre semanas buscando empleo desempleo indican que en el año
1996 existieron aproximadamente unas 8.4 semanas desempleadas en el Perú Urbano lo
cual, comparado con las 52 semanas disponibles al año indica que la proporción
de semanas desocupadas, para aquellos que han experimentado desempleo, ascendió al
16.1%. • Cuando se analizan datos de duración es necesario pensar en términos de probabilidades condicionales. Para obtener el instrumento adecuado de análisis se puede partir de la conocida función de distribución acumulativa de una variable. Esta probabilidad se define como la probabilidad que una variable aleatoria T sea menor que un valor determinado t25. F(t) = Pr (T£ t) La densidad de esta función viene dada por
f(t) = dF(t)/dt. Para el análisis
de duración conviene expresar esta distribución en términos de la
función de sobrevivencia que viene dada por
S(t) = 1- F(t) = Pr(T>t). En
particular, interesa expresar esta distribución en términos de una
función de riesgo dada por:
La función de riesgo[
l
Un instrumento empírico útil es la estimación del
estimador Kaplan - Meier, cuya función de sobrevivencia viene dada por la siguiente
expresión.
Donde hi es el número de episodios completos de desempleo y ni es
el número de episodios de desempleo que no se han completado o están
censorados en el periodo i. En este caso l
= hi/ni es la probabilidad que un episodio de desempleo termine en el periodo i dado
que duró hasta el periodo i. En el caso que exista más de un riesgo,
también se puede calcular los estimadores de Kaplan-Meier. En el caso de las
funciones de riesgo muestrales bastaría reemplazar el número de escapes por
los escapes por causas específicas y dividir entre las personas en riesgo en cada
momento. En nuestro caso interesa distinguir dos tipos de escapes: escapes al empleo y
escapes a la inactividad, dado que cada uno de ellos explica aproximadamente la mitad del
desempleo en el país26.
En base a la información del panel de 1996, se ha estimado esta
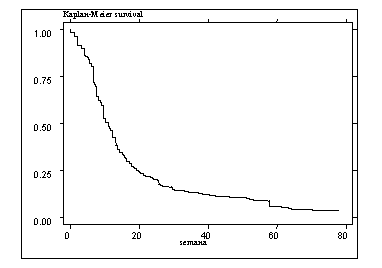
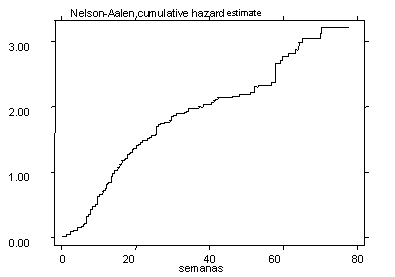
función de sobrevivencia total y por causas específicas las cuales se muestran
en el gráfico No. 6. Este gráfico indica que la probabilidad de sobrevivencia
en el desempleo baja rápidamente hasta que se arriba a 24 semanas aproximadamente
cuando llega al 0.20%. Sobre las 24 semanas la probabilidad de sobrevivencia se sigue
reduciendo pero a una menor tasa. En términos más sencillos existe una gran
proporción de desempleados que sale del desempleo en los primeros 6 meses. Sin
embargo, para aquellos que excedieron este limite, la tasa de salida del desempleo es muy
lenta.
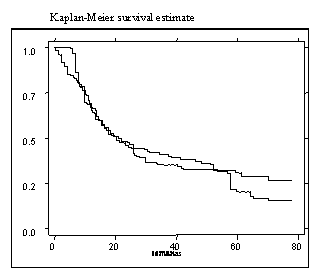
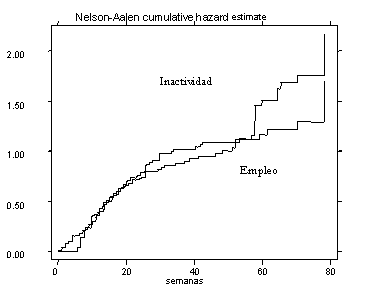
Si se realiza un análisis por causas específicas de escape,
dividiendo entre riesgos competidores hacia al empleo y hacia la inactividad, se encuentran
diferencias interesantes. La función de sobrevivencia de aquellos que terminan en la
inactividad desciende más rápidamente que la de aquellos que terminan en el
empleo a medida que transcurre el tiempo. En otras palabras, se incrementa la probabilidad
de salir del desempleo de aquellos que terminan en la inactividad en relación a
aquellos que terminan en el empleo.
Este tipo de análisis también se puede realizar para
subgrupos específicos como los pobres, los jóvenes, las mujeres, y los
cesantes, tal como se muestra en los gráficos de sobrevivencia de la parte C del
Anexo. En general, para todos los grupos observados existen diferentes comportamientos en
las probabilidades condicionales de terminar en la inactividad y la probabilidad condicional
de terminar en el empleo que se reflejan en la forma de estas funciones.
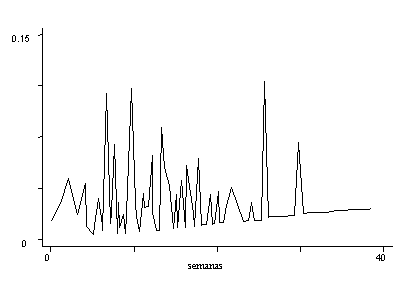
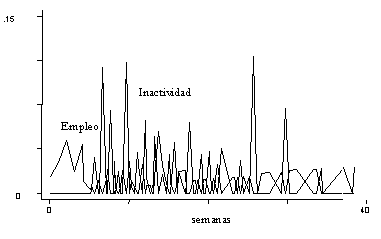
Otra forma de expresar estos mismos resultados es a través del
análisis de las tasas de riesgo, lo cual se realiza en el gráfico Nº 7,
tanto para la muestra total como para las de causas especificas. Este gráfico en
realidad es un poco difícil de analizar pues presenta mucho ruido en la medida en que
está afectado por diversos elementos. En ese sentido, un instrumento útil es
el análisis de las tasas integradas de riesgo que suelen suavizar el análisis
gráfico. Estas tasas integradas se muestran en el gráfico Nº 8 y en los
gráficos para grupos específicos de la sección B del Anexo. Gráfico 4.3 Sobrevivencia Total
Sobrevivencia según Salidas al Empleo o a la Inactividad
Gráfico 4.4
Gráfico 4.5
• El análisis realizado hasta aquí ha sido principalmente gráfico. Sin embargo, para establecer claramente como se comportan los riesgos de escape de desempleo es necesario ajustar una distribución paramétrica a esta data. En primer lugar, se estimó un modelo tradicional de riesgo único: el no desempleo o la salida del desempleo. Se decidió trabajar con la distribución Weibull que es la forma general de función exponencial por la cual la función de riesgo estimada tiene la siguiente forma:
donde g
> 0 y a
> 0 27. En particular se asumió una
especificación de riesgos proporcionales de la forma l
(
t)
= l
(
o)
eC
´B
, , donde l
(
o)
= a
ta
-1 es el riesgo en la
línea de base (baseline hazard), es el parámetro a ser estimado desde
la propia data y X es un vector de características individuales que explican la
duración del desempleo28. La función de riesgos muestra dependencia de la duración positiva (negativa) si a
>1(
a
<1)
.si a
=1, no existe dependencia de la duración.
En segundo lugar, la evidencia de que una fracción importante de
los episodios de desempleo terminen en la inactividad determina la necesidad de estimar
también un modelo de riesgos competidores. En este caso, siguiendo a Katz (1986) se
utiliza una especificación tipo Weibull de riesgos proporcionales con causas
específicas: empleo o inactividad. Las funciones de riesgo de empleo o de inactividad
para un individuo i con variables explicativas Xi se especifican de la siguiente manera:
para el riesgo de empleo y el de inactividad respectivamente y b1 y b2 son vectores de parámetros. En este caso, la probabilidad que un episodio de desempleo de un individuo j (Tuj) dure por lo menos hasta el periodo t, es la probabilidad conjunta de que la duración hasta el empleo (Tej) y la duración hasta la inactividad (Tij) duren ambas hasta el periodo t. La función de sobrevivencia es:
donde h
(t)= e
(t) + u
(t) . Reemplazando en esta ecuación e integrando
se obtiene que
En términos de estimación econométrica, según
Katz (1986) si la data fuera ordenada de la siguiente manera: los primeros k1 episodios en
un riesgo (empleo), los segundos k2 en otro riesgo (inactividad) y los restantes como
censorados, la función de verosimilitud puede ser escrita de la siguiente manera
donde
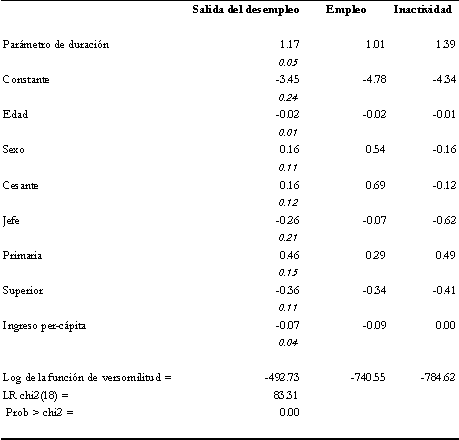
Cuadro 4.4 Nota: Los errores estándar de los
parámetros de la regresión aparecen en cursiva
__________________________________________________________________________________ 23 En la sección A del Anexo se indica algunos métodos alternativos para estimar la duración completa del desempleo en base a los datos de las encuestas. 24 El periodo de desempleo para los desempleados en el II trimestre del año se ha completado utilizando las preguntas sobre duración del desempleo, tiempo sin empleo y tiempo en el empleo actual. 25 En nuestro caso, t representa el momento o fecha en el cual termina el periodo de desempleo. 26 Para una discusión sobre el caso de riesgos competidores ver Kalbfleish y Prentice (1980). 27 Nótese que si a=1 esta función se convierte en exponencial. 28 En este caso, se han introducido las siguientes variables: sexo, edad, nivel educativo (a través de variables dicotómicas para la educación primaria, incluyendo a las personas con inicial o sin nivel educativo, y para la educación superior), experiencia laboral (si es cesante, es decir trabajó antes, o no), condición de jefe del hogar, ingreso del hogar per capita (en cientos de nuevos soles), y variables de control regionales (por las diferencias existentes en el mercado de trabajo que afectan la duración del desempleo). 29 Con la finalidad de estimar este modelo de dos riesgos usando la información del panel 96 se asumió que aquellos que habían terminado como inactivos lo hicieron en una fecha intermedia entre las dos encuestas (fecha de la entrevista más el tiempo hasta la observación siguiente por la proporción de desempleados que termina como inactivos). Lo mismo se hizo en el caso del grupo que consiguió empleo en el último trimestre. 30 Las tasas de riesgo (hazard ratios) y las tasas temporales (time ratios) estimadas se presentan en la sección D del Anexo. Las primeras reflejan el riesgo de salir, mientras las segundas dan una idea de la duración esperada del desempleo cuando se posee una característica determinada en relación a alguien que no la posee (por ejemplo ser cesantes en lugar de aspirantes). |