2.2 LA MEDICIÓN DE LA POBREZA

Existe una amplia literatura para medir la pobreza16. Por "medir la pobreza" se entiende el caracterizarla en términos de tres variables: la incidencia de la pobreza (el número de pobres), la intensidad de la pobreza (cuán pobres son los pobres, la diferencia entre el ingreso de los pobres y la línea de pobreza) y, finalmente, la severidad de la pobreza (distribución del ingreso al interior de los pobres o el grado de desigualdad entre los pobres).

Muchos investigadores han hecho los intentos de diseñar medidas amplias de pobreza que incorporen los tres aspectos antes mencionados17. Amartya Sen (1976) propuso condiciones ideales que debían cumplir los indicadores de pobreza para reflejar los cambios en la distribución del ingreso entre los pobres. Sen formuló dos axiomas que toda medida de pobreza debería satisfacer: el axioma de monotocidad y el axioma de transferencia. El primero de ellos, dice que, céteris paribus, una reducción en el ingreso de una persona que se encuentra por debajo de la línea de pobreza deberá aumentar el valor de la medida de pobreza. Por su parte, el segundo axioma, dice que, céteris paribus, una transferencia pura de ingreso de una persona que se encuentra por debajo de la línea de pobreza a cualquiera que tenga un nivel de ingreso más alto (puede ser también pobre), deberá de aumentar el valor de la medida de pobreza.

El indicador incidencia de la pobreza (H) viola ambos axiomas, mientras que el déficit agregado de pobreza (D) y el normalizado o la brecha de ingreso (I) violan el segundo axioma. H = p/n ; I = (å Gi )/p, para i=1,2,...p y Gi = gi /z = (z- yi )/z; donde: p representa el número de familias pobres, n es el total de familias, z es la línea de pobreza, yi es el ingreso de la familia i, gi es la brecha de ingreso con respecto a la línea de pobreza de la familia i.

Por lo que Sen deriva axiomáticamente un índice de pobreza que incorpora los tres indicadores basándose en una concepción ordinal de bienestar, que es una "suma ponderada normalizada de las brechas de ingreso individuales utilizando pesos no negativos"18. De manera, que su forma general es la siguiente:

donde: A es el parámetro de normalización y vi es el ponderador de gi.

Mediante la operacionalización de los siguientes axiomas la expresión anterior se transforma en el índice de pobreza de Sen (Ps). En primer lugar, mediante el "axioma de ponderaciones de rango ordinales" se especifica como se determina el coeficiente de ponderación vi que recibe el déficit de pobreza de cada individuo i: éste es igual al rango que cada individuo ocupa en el ordenamiento interpersonal de bienestar de los pobres. En segundo lugar, mediante el "axioma de bienestar monotónico", se especifica cómo ordenar a los pobres según su nivel de bienestar. se asume que este último depende del ingreso de tal manera que a un mayor ingreso corresponde un bienestar mayor; es decir, si Wi (y) representa el nivel de bienestar del individuo i, entonces par i, j cualesquiera, si xi > xj , se cumplirá que Wi (y) > Wj (y), y por lo tanto que vi < vj. Por último, mediante el "axioma de valor normalizado de pobreza" se especifica el proceso de normalización. este dice que si todos los pobres tuvieran el mismo ingreso, entonces el indicador de pobreza sería el producto de H por I, entonces P = H Y.

Según Sen, estos tres axiomas determinan unívocamente el siguiente índice de pobreza :

donde: G es el coeficiente de Gini de la distribución del ingreso para los pobres, es decir para i = 1,2,...p. Ps no sólo toma en cuenta el número de pobres y la brecha de ingresos, sino que además incluye consideraciones de desigualdad entre los pobres. Del índice Ps se desprende que si aumenta la proporción de pobres (H), si aumenta el déficit de pobreza (Y) o si aumenta la desigualdad en la distribución del ingreso de los pobres (G), aumenta el valor de Ps. Es decir, este índice cumple con todas las condiciones señaladas para un índice de pobreza.

Foster, Greer y Thorbecke (1984) construyen una familia de indicadores que permite conocer las tres variables mas importantes que caracterizan al grupo de los pobres. Ellos son: el índice de head-count (H), el índice de la brecha de la pobreza (HI) y la medida de desigualdad entre los pobres (P2).

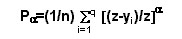
donde: a puede ser interpretado como una medida de sensibilidad a la pobreza, es decir, este coeficiente refleja la sensibilidad asignada por las personas a la distribución del ingreso o del gasto al interior de los pobres: mientras más alto sea a le da más énfasis a los más pobres.

Este índice toma la brecha de cada persona pobre como una fracción de la línea de pobreza (z-yi)/z elevada a una potencia a, y sumando sobre las unidades pobres.

Para valores de a>1, este índice no sólo toma en cuenta la incidencia y la intensidad de la pobreza, sino también es sensitivo al grado de desigualdad entre los pobres. Es decir, una transferencia de un sol a las unidades más pobres desde las menos pobres disminuirá el índice de pobreza

Si a=2, el índice es igual a:

Pa=2 = HI2 /H + [(H-HI)2/H ]C2

donde: C es el coeficiente de la variación del consumo entre los pobres.

Esta medida puede ser interpretada como la suma de dos componentes: una cantidad debido a la brecha de pobreza y otra debido a la desigualdad entre los pobres. Es una medida de desigualdad entre los pobres, la que crece con el cuadrado de la distancia entre el gasto de cada pobre y la línea de pobreza. A mayor desigualdad entre los pobres, mayor es el valor de Pa=2. El índice tiene la ventaja para comparar políticas que tienen el objetivo de mejorar la situación de los más pobres. Sin embargo, no es tan fácil de interpretar como HI o H, constituyendo una limitación para propósitos expositivos.

Si a=0 la medida de la pobreza Pa=0 = H = p/n, donde H es el ratio head-count (población pobre), significa que la medida es indiferente a la intensidad de la pobreza. Es decir, no brinda información sobre qué tan lejos de la línea de pobreza están los pobres, tampoco es útil para realizar análisis de impacto de ciertas políticas sobre los pobres. Es de fácil exposición y puede permitir apreciar la tendencia de la pobreza en tiempo.

Si a=1, el índice de pobreza es igual a: Pa=1 = H.I, donde I, es el ratio de la brecha ingreso (gasto). Este índice (HI) si toma en cuenta la intensidad de la pobreza y la incidencia de la pobreza. Puede ser utilizado para calcular el monto de recursos que se necesita transferir a los pobres para erradicar la pobreza (bajo perfecta focalización. Esta transferencia es la sumatoria de todas las brechas de pobreza en una población: si cada brecha es ajustada hacia la línea de la pobreza, el costo sería igual a:

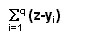
No obstante esta ventaja, este índice es insensitiva a la distribución del ingreso entre los pobres. el hecho de transferir ingresos desde un individuo más pobre a uno menos pobre dejará invariable HI.

Las medidas FGT son aditivas desagregables (puede ser descompuesto aditivamente), es decir, si los ingresos de un subgrupo varían y el resto no, la pobreza debería moverse en la misma dirección. De esta manera, si en la población en estudio existen m grupos, la pobreza puede ser expresada como el promedio ponderado de los niveles de pobreza de subgrupos. Así el indicador sería:

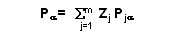
donde: Pja es el índice de pobreza del grupo j, y Zj es el peso de la población del grupo j (j= 1,2,....m), å Zj = 1.

Las FGT toman la brecha de pobreza como una proporción de la línea de pobreza, debido a ello las medidas FGT están en un rango de 0 a 1. A medida que a aumenta, las FGT llegan a ser más pequeñas.

Las medidas FGT son muy útiles para realizar comparaciones de pobreza. Por ejemplo, las características de la pobreza nos permitiría conocer cómo ella varía entre los sub grupos de la sociedad (región de residencia, categoría ocupacional, niveles de educación alcanzados). Igualmente, nos sirve para evaluar como los patrones regionales de pobreza cambian, y como esto afecta a la pobreza agregada. En general, podemos decir que las medidas FGT nos proporciona indicadores ordinales de pobreza factibles de ser descompuestos aditivamente, por lo que son ideales para hacer inferencias de corte transversal como se series de tiempo. En este caso se deben calcular las medidas FGT para cada periodo (por región o grupo socioeconómico) y luego compararlas.